Chapter 13 Assignment 3: Demand Function Estimation I

13.1 Simulate data

We simulate data from a discrete choice model. There are \(T\) markets and each market has \(N\) consumers. There are \(J\) products and the indirect utility of consumer \(i\) in market \(t\) for product \(j\) is: \[ u_{itj} = \beta_{it}' x_j + \alpha_{it} p_{jt} + \xi_{jt} + \epsilon_{ijt}, \] where \(\epsilon_{ijt}\) is an i.i.d. type-I extreme random variable. \(x_j\) is \(K\)-dimensional observed characteristics of the product. \(p_{jt}\) is the retail price of the product in the market.

\(\xi_{jt}\) is product-market specific fixed effect. \(p_{jt}\) can be correlated with \(\xi_{jt}\) but \(x_{jt}\)s are independent of \(\xi_{jt}\). \(j = 0\) is an outside option whose indirect utility is: \[ u_{it0} = \epsilon_{i0t}, \] where \(\epsilon_{i0t}\) is an i.i.d. type-I extreme random variable.

\(\beta_{it}\) and \(\alpha_{it}\) are different across consumers, and they are distributed as: \[ \beta_{itk} = \beta_{0k} + \sigma_k \nu_{itk}, \] \[ \alpha_{it} = - \exp(\mu + \omega \upsilon_{it}) = - \exp(\mu + \frac{\omega^2}{2}) + [- \exp(\mu + \omega \upsilon_{it}) + \exp(\mu + \frac{\omega^2}{2})] \equiv \alpha_0 + \tilde{\alpha}_{it}, \] where \(\nu_{itk}\) for \(k = 1, \cdots, K\) and \(\upsilon_{it}\) are i.i.d. standard normal random variables. \(\alpha_0\) is the mean of \(\alpha_i\) and \(\tilde{\alpha}_i\) is the deviation from the mean.

Given a choice set in the market, \(\mathcal{J}_t \cup \{0\}\), a consumer chooses the alternative that maximizes her utility: \[ q_{ijt} = 1\{u_{ijt} = \max_{k \in \mathcal{J}_t \cup \{0\}} u_{ikt}\}. \] The choice probability of product \(j\) for consumer \(i\) in market \(t\) is: \[ \sigma_{jt}(p_t, x_t, \xi_t) = \mathbb{P}\{u_{ijt} = \max_{k \in \mathcal{J}_t \cup \{0\}} u_{ikt}\}. \]

Suppose that we only observe the share data: \[ s_{jt} = \frac{1}{N} \sum_{i = 1}^N q_{ijt}, \] along with the product-market characteristics \(x_{jt}\) and the retail prices \(p_{jt}\) for \(j \in \mathcal{J}_t \cup \{0\}\) for \(t = 1, \cdots, T\). We do not observe the choice data \(q_{ijt}\) nor shocks \(\xi_{jt}, \nu_{it}, \upsilon_{it}, \epsilon_{ijt}\).

In this assignment, we consider a model with \(\xi_{jt} = 0\), i.e., the model without the unobserved fixed effects. However, the code to simulate data should be written for general \(\xi_{jt}\), so that we can use the same code in the next assignment in which we consider a model with the unobserved fixed effects.

  1. Set the seed, constants, and parameters of interest as follows.
# set the seed
set.seed(1)
# number of products
J <- 10
# dimension of product characteristics including the intercept
K <- 3
# number of markets
T <- 100
# number of consumers per market
N <- 500
# number of Monte Carlo
L <- 500
# set parameters of interests
beta <- rnorm(K); 
beta[1] <- 4
beta
## [1]  4.0000000  0.1836433 -0.8356286
sigma <- abs(rnorm(K)); sigma
## [1] 1.5952808 0.3295078 0.8204684
mu <- 0.5
omega <- 1

Generate the covariates as follows.

The product-market characteristics: \[ x_{j1} = 1, x_{jk} \sim N(0, \sigma_x), k = 2, \cdots, K, \] where \(\sigma_x\) is referred to as sd_x in the code.

The product-market-specific unobserved fixed effect: \[ \xi_{jt} = 0. \] The marginal cost of product \(j\) in market \(t\): \[ c_{jt} \sim \text{logNormal}(0, \sigma_c), \] where \(\sigma_c\) is referred to as sd_c in the code.

The retail price: \[ p_{jt} - c_{jt} \sim \text{logNorm}(\gamma \xi_{jt}, \sigma_p), \] where \(\gamma\) is referred to as price_xi and \(\sigma_p\) as sd_p in the code. This price is not the equilibrium price. We will revisit this point in a subsequent assignment.

The value of the auxiliary parameters are set as follows:

# set auxiliary parameters
price_xi <- 1
prop_jt <- 0.6
sd_x <- 0.5
sd_c <- 0.05
sd_p <- 0.05
  1. X is the data frame such that a row contains the characteristics vector \(x_{j}\) of a product and columns are product index and observed product characteristics. The dimension of the characteristics \(K\) is specified above. Add the row of the outside option whose index is \(0\) and all the characteristics are zero.
# make product characteristics data
X <- 
  matrix(
    sd_x * rnorm(J * (K - 1)), 
    nrow = J
    )
X <- 
  cbind(
    rep(1, J), 
    X
    )
colnames(X) <- paste("x", 1:K, sep = "_")
X <- 
  data.frame(
    j = 1:J,
    X
    ) %>%
  tibble::as_tibble()
# add outside option
X <- 
  rbind(
    rep(0, dim(X)[2]),
    X
    ) 
X
## # A tibble: 11 × 4
##        j   x_1     x_2      x_3
##    <dbl> <dbl>   <dbl>    <dbl>
##  1     0     0  0       0      
##  2     1     1  0.244  -0.00810
##  3     2     1  0.369   0.472  
##  4     3     1  0.288   0.411  
##  5     4     1 -0.153   0.297  
##  6     5     1  0.756   0.459  
##  7     6     1  0.195   0.391  
##  8     7     1 -0.311   0.0373 
##  9     8     1 -1.11   -0.995  
## 10     9     1  0.562   0.310  
## 11    10     1 -0.0225 -0.0281
  1. M is the data frame such that a row contains the price \(\xi_{jt}\), marginal cost \(c_{jt}\), and price \(p_{jt}\). After generating the variables, drop 1 - prop_jt products from each market using dplyr::sample_frac function. The variation in the available products is important for the identification of the distribution of consumer-level unobserved heterogeneity. Add the row of the outside option to each market whose index is \(0\) and all the variables take value zero.
# make market-product data
M <- 
  expand.grid(
    j = 1:J, 
    t = 1:T
    ) %>%
  tibble::as_tibble() %>%
  dplyr::mutate(
    xi = 0,
    c = exp(sd_c * rnorm(J*T)),
    p = exp(price_xi * xi + sd_p * rnorm(J*T)) + c
  ) 
M <- 
  M %>%
  dplyr::group_by(t) %>%
  dplyr::sample_frac(prop_jt) %>%
  dplyr::ungroup()
# add outside option
outside <- 
  data.frame(
    j = 0, 
    t = 1:T, 
    xi = 0, 
    c = 0, 
    p = 0
    )
M <- 
  rbind(
    M,
    outside
    ) %>%
  dplyr::arrange(
    t, 
    j
    )
M
## # A tibble: 700 × 5
##        j     t    xi     c     p
##    <dbl> <int> <dbl> <dbl> <dbl>
##  1     0     1     0 0      0   
##  2     2     1     0 0.929  1.97
##  3     3     1     0 0.976  1.91
##  4     4     1     0 1.02   2.05
##  5     6     1     0 0.995  1.98
##  6     7     1     0 1.02   1.98
##  7     8     1     0 0.997  1.99
##  8     0     2     0 0      0   
##  9     1     2     0 0.980  1.97
## 10     4     2     0 1.04   2.04
## # ℹ 690 more rows
  1. Generate the consumer-level heterogeneity. V is the data frame such that a row contains the vector of shocks to consumer-level heterogeneity, \((\nu_{i}', \upsilon_i)\). They are all i.i.d. standard normal random variables.
# make consumer-market data
V <- 
  matrix(
    rnorm(N * T * (K + 1)), 
    nrow = N * T
    ) 
colnames(V) <- c(paste("v_x", 1:K, sep = "_"), "v_p")
V <- 
  data.frame(
    expand.grid(
      i = 1:N, 
      t = 1:T
      ),
    V
    ) %>%
  tibble::as_tibble()
V
## # A tibble: 50,000 × 6
##        i     t  v_x_1   v_x_2  v_x_3     v_p
##    <int> <int>  <dbl>   <dbl>  <dbl>   <dbl>
##  1     1     1  1.32  -0.0670 -0.758 -0.590 
##  2     2     1  0.930  1.34    1.16   0.0684
##  3     3     1  1.08   0.768  -0.725 -0.130 
##  4     4     1 -0.300  0.156  -0.641 -0.896 
##  5     5     1  1.04   1.17   -0.224  1.31  
##  6     6     1  0.709 -0.286   0.948  1.15  
##  7     7     1 -1.27   0.193  -0.212 -0.156 
##  8     8     1 -0.932 -0.780   1.49  -0.362 
##  9     9     1  1.37  -0.205   0.594 -0.998 
## 10    10     1 -0.461 -0.834   0.221 -1.62  
## # ℹ 49,990 more rows
  1. Join X, M, V using dplyr::left_join and name it df. df is the data frame such that a row contains variables for a consumer about a product that is available in a market.
# make choice data
df <- 
  expand.grid(
    t = 1:T, 
    i = 1:N, 
    j = 0:J
    ) %>%
  tibble::as_tibble() %>%
  dplyr::left_join(
    V, 
    by = c("i", "t")
    ) %>%
  dplyr::left_join(
    X, 
    by = c("j")
    ) %>%
  dplyr::left_join(
    M, 
    by = c("j", "t")
    ) %>%
  dplyr::filter(!is.na(p)) %>%
  dplyr::arrange(
    t, 
    i, 
    j
    )
df
## # A tibble: 350,000 × 13
##        t     i     j v_x_1   v_x_2  v_x_3     v_p   x_1    x_2     x_3    xi     c
##    <int> <int> <dbl> <dbl>   <dbl>  <dbl>   <dbl> <dbl>  <dbl>   <dbl> <dbl> <dbl>
##  1     1     1     0 1.32  -0.0670 -0.758 -0.590      0  0      0          0 0    
##  2     1     1     2 1.32  -0.0670 -0.758 -0.590      1  0.369  0.472      0 0.929
##  3     1     1     3 1.32  -0.0670 -0.758 -0.590      1  0.288  0.411      0 0.976
##  4     1     1     4 1.32  -0.0670 -0.758 -0.590      1 -0.153  0.297      0 1.02 
##  5     1     1     6 1.32  -0.0670 -0.758 -0.590      1  0.195  0.391      0 0.995
##  6     1     1     7 1.32  -0.0670 -0.758 -0.590      1 -0.311  0.0373     0 1.02 
##  7     1     1     8 1.32  -0.0670 -0.758 -0.590      1 -1.11  -0.995      0 0.997
##  8     1     2     0 0.930  1.34    1.16   0.0684     0  0      0          0 0    
##  9     1     2     2 0.930  1.34    1.16   0.0684     1  0.369  0.472      0 0.929
## 10     1     2     3 0.930  1.34    1.16   0.0684     1  0.288  0.411      0 0.976
## # ℹ 349,990 more rows
## # ℹ 1 more variable: p <dbl>
  1. Draw a vector of preference shocks e whose length is the same as the number of rows of df.
# draw idiosyncratic shocks
e <- evd::rgev(dim(df)[1])
head(e)
## [1]  0.32969177 -1.03771238  1.41496338  5.02048718 -0.01302806  0.57956001
  1. Write a function compute_indirect_utility(df, beta, sigma, mu, omega) that returns a vector whose element is the mean indirect utility of a product for a consumer in a market. The output should have the same length with \(e\).
# compute indirect utility
u <- 
  compute_indirect_utility(
    df, 
    beta, 
    sigma, 
    mu, 
    omega
    )
head(u)
##             u
## [1,] 0.000000
## [2,] 3.681882
## [3,] 3.807728
## [4,] 3.779036
## [5,] 3.764454
## [6,] 4.193113
  1. Write a function compute_choice(X, M, V, e, beta, sigma, mu, omega) that first construct df from X, M, V, second call compute_indirect_utility to obtain the vector of mean indirect utilities u, third compute the choice vector q based on the vector of mean indirect utilities and e, and finally return the data frame to which u and q are added as columns.
# compute choice
df_choice <- 
  compute_choice(
    X, 
    M, 
    V, 
    e, 
    beta, 
    sigma, 
    mu, 
    omega
    )
df_choice
## # A tibble: 350,000 × 16
##        t     i     j v_x_1   v_x_2  v_x_3     v_p   x_1    x_2     x_3    xi     c
##    <int> <int> <dbl> <dbl>   <dbl>  <dbl>   <dbl> <dbl>  <dbl>   <dbl> <dbl> <dbl>
##  1     1     1     0 1.32  -0.0670 -0.758 -0.590      0  0      0          0 0    
##  2     1     1     2 1.32  -0.0670 -0.758 -0.590      1  0.369  0.472      0 0.929
##  3     1     1     3 1.32  -0.0670 -0.758 -0.590      1  0.288  0.411      0 0.976
##  4     1     1     4 1.32  -0.0670 -0.758 -0.590      1 -0.153  0.297      0 1.02 
##  5     1     1     6 1.32  -0.0670 -0.758 -0.590      1  0.195  0.391      0 0.995
##  6     1     1     7 1.32  -0.0670 -0.758 -0.590      1 -0.311  0.0373     0 1.02 
##  7     1     1     8 1.32  -0.0670 -0.758 -0.590      1 -1.11  -0.995      0 0.997
##  8     1     2     0 0.930  1.34    1.16   0.0684     0  0      0          0 0    
##  9     1     2     2 0.930  1.34    1.16   0.0684     1  0.369  0.472      0 0.929
## 10     1     2     3 0.930  1.34    1.16   0.0684     1  0.288  0.411      0 0.976
## # ℹ 349,990 more rows
## # ℹ 4 more variables: p <dbl>, u <dbl>, e <dbl>, q <dbl>
summary(df_choice)
##        t                i               j              v_x_1          
##  Min.   :  1.00   Min.   :  1.0   Min.   : 0.000   Min.   :-4.302781  
##  1st Qu.: 25.75   1st Qu.:125.8   1st Qu.: 2.000   1st Qu.:-0.683141  
##  Median : 50.50   Median :250.5   Median : 5.000   Median : 0.001562  
##  Mean   : 50.50   Mean   :250.5   Mean   : 4.791   Mean   :-0.002669  
##  3rd Qu.: 75.25   3rd Qu.:375.2   3rd Qu.: 8.000   3rd Qu.: 0.669657  
##  Max.   :100.00   Max.   :500.0   Max.   :10.000   Max.   : 3.809895  
##      v_x_2               v_x_3                v_p                 x_1        
##  Min.   :-4.542122   Min.   :-3.957618   Min.   :-4.218131   Min.   :0.0000  
##  1st Qu.:-0.680086   1st Qu.:-0.673321   1st Qu.:-0.671449   1st Qu.:1.0000  
##  Median : 0.002374   Median : 0.004941   Median : 0.001083   Median :1.0000  
##  Mean   :-0.000890   Mean   : 0.003589   Mean   :-0.002011   Mean   :0.8571  
##  3rd Qu.: 0.673194   3rd Qu.: 0.676967   3rd Qu.: 0.671318   3rd Qu.:1.0000  
##  Max.   : 4.313621   Max.   : 4.244194   Max.   : 4.017246   Max.   :1.0000  
##       x_2                x_3                xi          c                p        
##  Min.   :-1.10735   Min.   :-0.9947   Min.   :0   Min.   :0.0000   Min.   :0.000  
##  1st Qu.:-0.15269   1st Qu.: 0.0000   1st Qu.:0   1st Qu.:0.9404   1st Qu.:1.913  
##  Median : 0.19492   Median : 0.2970   Median :0   Median :0.9841   Median :1.981  
##  Mean   : 0.05989   Mean   : 0.1128   Mean   :0   Mean   :0.8560   Mean   :1.712  
##  3rd Qu.: 0.36916   3rd Qu.: 0.3911   3rd Qu.:0   3rd Qu.:1.0260   3rd Qu.:2.039  
##  Max.   : 0.75589   Max.   : 0.4719   Max.   :0   Max.   :1.2099   Max.   :2.293  
##        u                  e                 q         
##  Min.   :-190.479   Min.   :-2.6364   Min.   :0.0000  
##  1st Qu.:  -2.177   1st Qu.:-0.3301   1st Qu.:0.0000  
##  Median :   0.000   Median : 0.3635   Median :0.0000  
##  Mean   :  -1.291   Mean   : 0.5763   Mean   :0.1429  
##  3rd Qu.:   1.978   3rd Qu.: 1.2418   3rd Qu.:0.0000  
##  Max.   :  10.909   Max.   :14.0966   Max.   :1.0000
  1. Write a function compute_share(X, M, V, e, beta, sigma, mu, omega) that first construct df from X, M, V, second call compute_choice to obtain a data frame with u and q, third compute the share of each product at each market s and the log difference in the share from the outside option, \(\ln(s_{jt}/s_{0t})\), denoted by y, and finally return the data frame that is summarized at the product-market level, dropped consumer-level variables, and added s and y.
# compute share
df_share <-
  compute_share(
    X, 
    M, 
    V, 
    e, 
    beta, 
    sigma, 
    mu, 
    omega
    )
df_share
## # A tibble: 700 × 11
##        t     j   x_1    x_2      x_3    xi     c     p     q     s       y
##    <int> <dbl> <dbl>  <dbl>    <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>   <dbl>
##  1     1     0     0  0      0           0 0      0      144 0.288  0     
##  2     1     2     1  0.369  0.472       0 0.929  1.97    47 0.094 -1.12  
##  3     1     3     1  0.288  0.411       0 0.976  1.91    37 0.074 -1.36  
##  4     1     4     1 -0.153  0.297       0 1.02   2.05    35 0.07  -1.41  
##  5     1     6     1  0.195  0.391       0 0.995  1.98    60 0.12  -0.875 
##  6     1     7     1 -0.311  0.0373      0 1.02   1.98    44 0.088 -1.19  
##  7     1     8     1 -1.11  -0.995       0 0.997  1.99   133 0.266 -0.0795
##  8     2     0     0  0      0           0 0      0      170 0.34   0     
##  9     2     1     1  0.244 -0.00810     0 0.980  1.97    84 0.168 -0.705 
## 10     2     4     1 -0.153  0.297       0 1.04   2.04    35 0.07  -1.58  
## # ℹ 690 more rows
summary(df_share)
##        t                j               x_1              x_2          
##  Min.   :  1.00   Min.   : 0.000   Min.   :0.0000   Min.   :-1.10735  
##  1st Qu.: 25.75   1st Qu.: 2.000   1st Qu.:1.0000   1st Qu.:-0.15269  
##  Median : 50.50   Median : 5.000   Median :1.0000   Median : 0.19492  
##  Mean   : 50.50   Mean   : 4.791   Mean   :0.8571   Mean   : 0.05989  
##  3rd Qu.: 75.25   3rd Qu.: 8.000   3rd Qu.:1.0000   3rd Qu.: 0.36916  
##  Max.   :100.00   Max.   :10.000   Max.   :1.0000   Max.   : 0.75589  
##       x_3                xi          c                p               q         
##  Min.   :-0.9947   Min.   :0   Min.   :0.0000   Min.   :0.000   Min.   : 26.00  
##  1st Qu.: 0.0000   1st Qu.:0   1st Qu.:0.9404   1st Qu.:1.913   1st Qu.: 43.00  
##  Median : 0.2970   Median :0   Median :0.9841   Median :1.981   Median : 52.00  
##  Mean   : 0.1128   Mean   :0   Mean   :0.8560   Mean   :1.712   Mean   : 71.43  
##  3rd Qu.: 0.3911   3rd Qu.:0   3rd Qu.:1.0260   3rd Qu.:2.039   3rd Qu.: 73.00  
##  Max.   : 0.4719   Max.   :0   Max.   :1.2099   Max.   :2.293   Max.   :195.00  
##        s                y           
##  Min.   :0.0520   Min.   :-1.89354  
##  1st Qu.:0.0860   1st Qu.:-1.35812  
##  Median :0.1040   Median :-1.16644  
##  Mean   :0.1429   Mean   :-0.99214  
##  3rd Qu.:0.1460   3rd Qu.:-0.81801  
##  Max.   :0.3900   Max.   : 0.05196

13.2 Estimate the parameters

  1. Estimate the parameters assuming there is no consumer-level heterogeneity, i.e., by assuming: \[ \ln \frac{s_{jt}}{s_{0t}} = \beta' x_{jt} + \alpha p_{jt}. \] This can be implemented using lm function. Print out the estimate results.
## 
## Call:
## lm(formula = y ~ -1 + x_1 + x_2 + x_3 + p, data = df_share)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.57415 -0.09781  0.00000  0.10491  0.51149 
## 
## Coefficients:
##     Estimate Std. Error t value Pr(>|t|)    
## x_1  1.20614    0.18150   6.646 6.10e-11 ***
## x_2  0.21995    0.02841   7.741 3.49e-14 ***
## x_3 -0.92818    0.03364 -27.589  < 2e-16 ***
## p   -1.12982    0.09086 -12.435  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.1677 on 696 degrees of freedom
## Multiple R-squared:  0.9778, Adjusted R-squared:  0.9777 
## F-statistic:  7678 on 4 and 696 DF,  p-value: < 2.2e-16

We estimate the model using simulated share.

When optimizing an objective function that uses the Monte Carlo simulation, it is important to keep the realizations of the shocks the same across the evaluations of the objective function. If the realization of the shocks differ across the objective function evaluations, the optimization algorithm will not converge because it cannot distinguish the change in the value of the objective function due to the difference in the parameters and the difference in the realized shocks.

The best practice to avoid this problem is to generate the shocks outside the optimization algorithm as in the current case. If the size of the shocks can be too large to store in the memory, the second best practice is to make sure to set the seed inside the optimization algorithm so that the realized shocks are the same across function evaluations.

  1. For this reason, we first draw Monte Carlo consumer-level heterogeneity V_mcmc and Monte Carlo preference shocks e_mcmc. The number of simulations is L. This does not have to be the same with the actual number of consumers N.
# mixed logit estimation
## draw mcmc V
V_mcmc <- 
  matrix(
    rnorm(L * T * (K + 1)), 
    nrow = L * T
    ) 
colnames(V_mcmc) <- c(paste("v_x", 1:K, sep = "_"), "v_p")
V_mcmc <- 
  data.frame(
    expand.grid(
      i = 1:L, 
      t = 1:T
      ),
    V_mcmc
    ) %>%
  tibble::as_tibble() 
V_mcmc
## # A tibble: 50,000 × 6
##        i     t   v_x_1  v_x_2   v_x_3    v_p
##    <int> <int>   <dbl>  <dbl>   <dbl>  <dbl>
##  1     1     1 -0.715  -0.798 -0.548   1.09 
##  2     2     1  0.0243 -0.943 -1.88    0.471
##  3     3     1 -0.183   0.660  0.669   1.45 
##  4     4     1  0.0207  3.36  -0.363   1.58 
##  5     5     1 -1.94    0.221  1.02    0.943
##  6     6     1  0.876  -0.636  0.0432  0.324
##  7     7     1  1.96   -0.195 -0.0950  1.39 
##  8     8     1  1.11    0.571  1.77    0.497
##  9     9     1  1.45    0.154  1.96    0.740
## 10    10     1 -1.00   -0.413  0.0542 -0.469
## # ℹ 49,990 more rows
## draw mcmc e
df_mcmc <- 
  expand.grid(
    t = 1:T, 
    i = 1:L, 
    j = 0:J
    ) %>%
  tibble::as_tibble() %>%
  dplyr::left_join(
    V_mcmc, 
    by = c("i", "t")
    ) %>%
  dplyr::left_join(
    X, 
    by = c("j")
    ) %>%
  dplyr::left_join(
    M, 
    by = c("j", "t")
    ) %>%
  dplyr::filter(!is.na(p)) %>%
  dplyr::arrange(
    t, 
    i, 
    j
    )
# draw idiosyncratic shocks
e_mcmc <- evd::rgev(dim(df_mcmc)[1])
head(e_mcmc)
## [1]  0.265602821  0.652183731 -0.006127627 -0.317288366  3.145022297 -1.277026910
  1. Use compute_share to check the simulated share at the true parameter using the Monte Carlo shocks. Remember that the number of consumers should be set at L instead of N.
df_share_mcmc
## # A tibble: 700 × 11
##        t     j   x_1    x_2      x_3    xi     c     p     q     s      y
##    <int> <dbl> <dbl>  <dbl>    <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>  <dbl>
##  1     1     0     0  0      0           0 0      0      171 0.342  0    
##  2     1     2     1  0.369  0.472       0 0.929  1.97    46 0.092 -1.31 
##  3     1     3     1  0.288  0.411       0 0.976  1.91    37 0.074 -1.53 
##  4     1     4     1 -0.153  0.297       0 1.02   2.05    38 0.076 -1.50 
##  5     1     6     1  0.195  0.391       0 0.995  1.98    38 0.076 -1.50 
##  6     1     7     1 -0.311  0.0373      0 1.02   1.98    52 0.104 -1.19 
##  7     1     8     1 -1.11  -0.995       0 0.997  1.99   118 0.236 -0.371
##  8     2     0     0  0      0           0 0      0      194 0.388  0    
##  9     2     1     1  0.244 -0.00810     0 0.980  1.97    62 0.124 -1.14 
## 10     2     4     1 -0.153  0.297       0 1.04   2.04    37 0.074 -1.66 
## # ℹ 690 more rows
  1. Vectorize the parameters to a vector theta because optim requires the maximiand to be a vector.
# set parameters
theta <- 
  c(
    beta, 
    sigma, 
    mu, 
    omega
    )
theta
## [1]  4.0000000  0.1836433 -0.8356286  1.5952808  0.3295078  0.8204684  0.5000000
## [8]  1.0000000
  1. Write a function compute_nlls_objective_a3(theta, df_share, X, M, V_mcmc, e_mcmc) that first computes the simulated share and then compute the mean-squared error between the share data.
nlls_objective
## [1] 0.0004815657
  1. Draw a graph of the objective function that varies each parameter from 0.5, 0.6, \(\cdots\), 1.5 of the true value. First try with the actual shocks V and e and then try with the Monte Carlo shocks V_mcmc and e_mcmc. You will some of the graph does not look good with the Monte Carlo shocks. It will cause the approximation error.

Because this takes time, you may want to parallelize the computation using %dopar functionality of foreach loop. To do so, first install doParallel package and then load it and register the workers as follows:

registerDoParallel()

This automatically detect the number of cores available at your computer and registers them as the workers. Then, you only have to change %do% to %dopar in the foreach loop as follows:

foreach (
  i = 1:4
  ) %dopar% {
    # this part is parallelized
    y <- 2 * i
    return(y)
}
## [[1]]
## [1] 2
## 
## [[2]]
## [1] 4
## 
## [[3]]
## [1] 6
## 
## [[4]]
## [1] 8

In windows, you may have to explicitly pass packages, functions, and data to the worker by using .export and .packages options as follows:

temp_func <- 
  function(x) {
    y <- 2 * x
    return(y)
}
foreach (
  i = 1:4, 
  .export = "temp_func",
  .packages = "magrittr"
  ) %dopar% {
    # this part is parallelized
    y <- temp_func(i)
    return(y)
}
## Warning in e$fun(obj, substitute(ex), parent.frame(), e$data): already exporting
## variable(s): temp_func
## [[1]]
## [1] 2
## 
## [[2]]
## [1] 4
## 
## [[3]]
## [1] 6
## 
## [[4]]
## [1] 8

If you have called a function in a package in this way dplyr::mutate, then you will not have to pass dplyr by .packages option. This is one of the reasons why I prefer to explicitly call the package every time I call a function. If you have compiled your functions in a package, you will just have to pass the package as follows:

# this function is compiled in the package EmpiricalIO
# temp_func <- function(x) {
#   y <- 2 * x
#   return(y)
# }
foreach (
  i = 1:4, 
  .packages = c(
    "EmpiricalIO",
    "magrittr")
  ) %dopar% {
    # this part is parallelized
    y <- temp_func(i)
    return(y)
}
## [[1]]
## [1] 2
## 
## [[2]]
## [1] 4
## 
## [[3]]
## [1] 6
## 
## [[4]]
## [1] 8

The graphs with the true shocks:

## [[1]]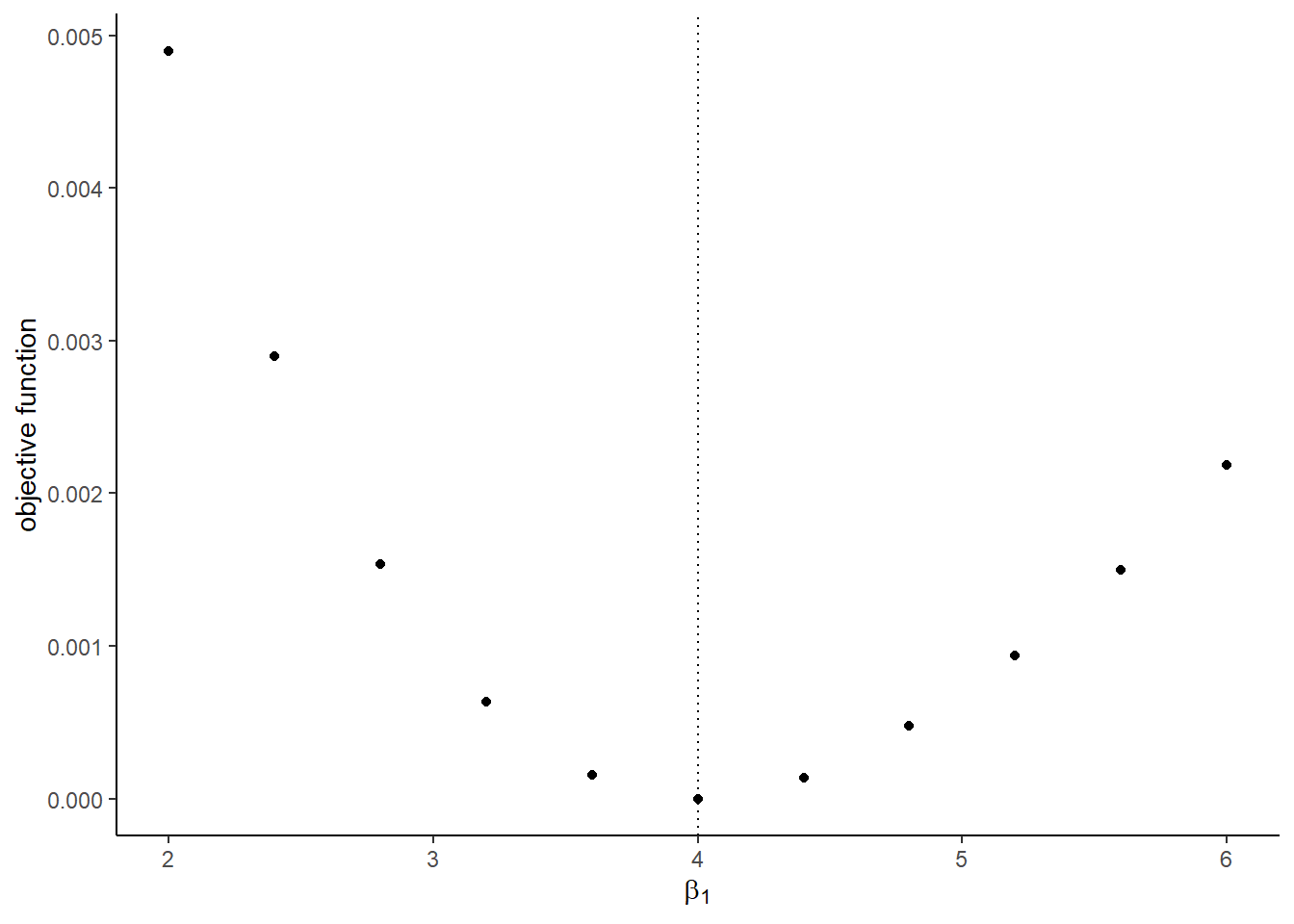
## Warning: Using the `size` aesthetic with geom_segment was deprecated in ggplot2 3.4.0.
## ℹ Please use the `linewidth` aesthetic instead.
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_lifecycle_warnings()` to see where this warning was generated.

## 
## [[2]]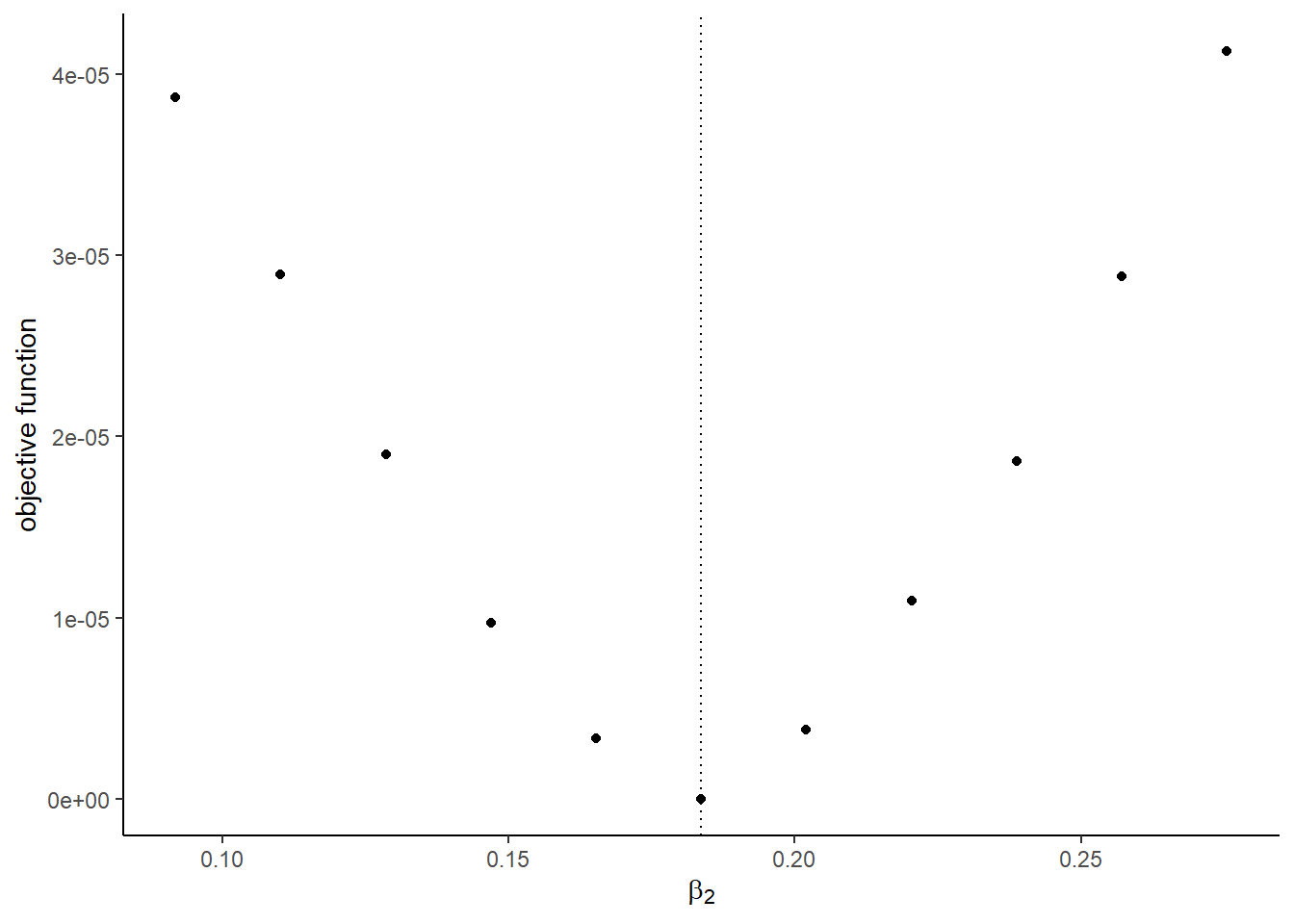

## 
## [[3]]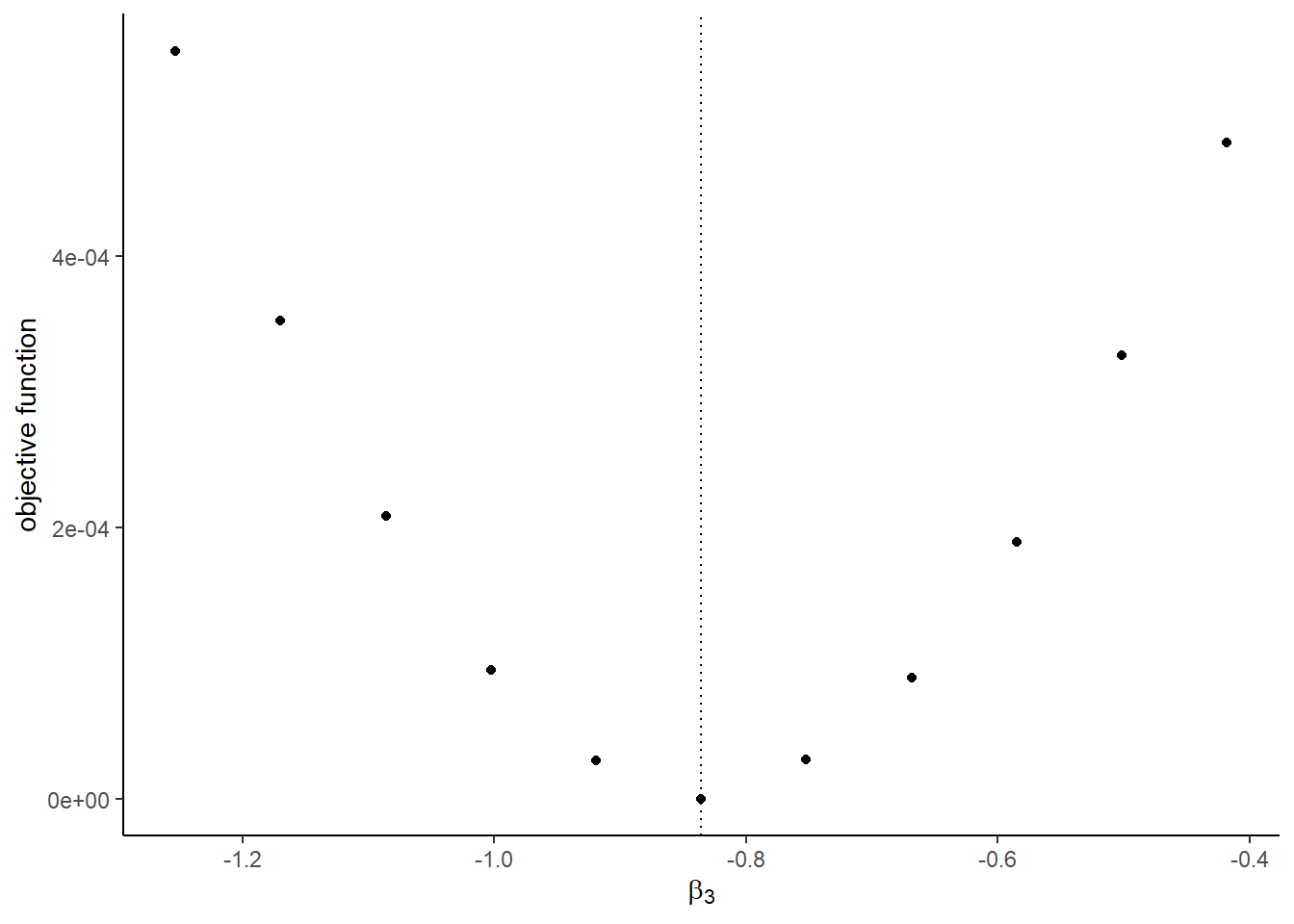

## 
## [[4]]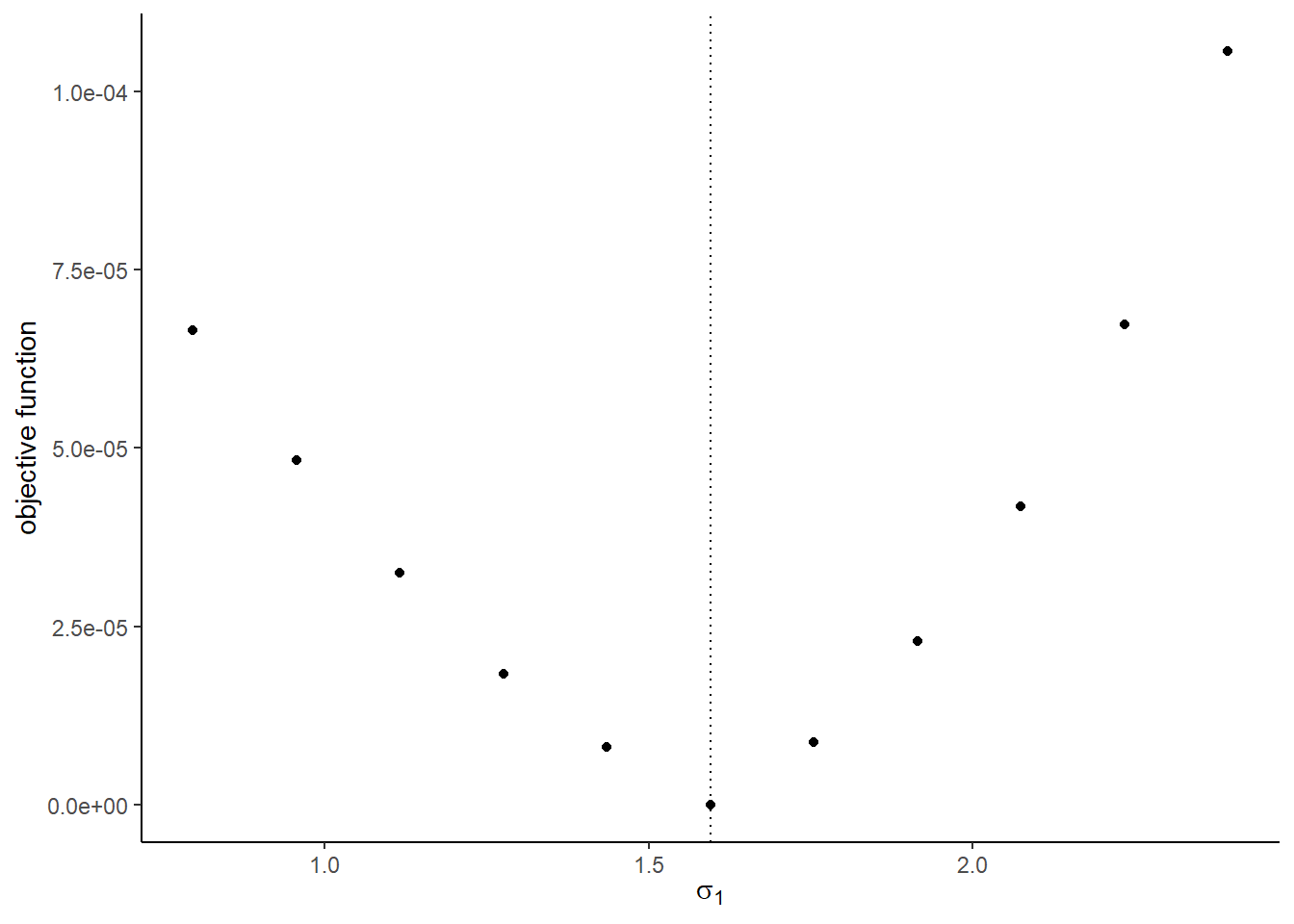

## 
## [[5]]

## 
## [[6]]

## 
## [[7]]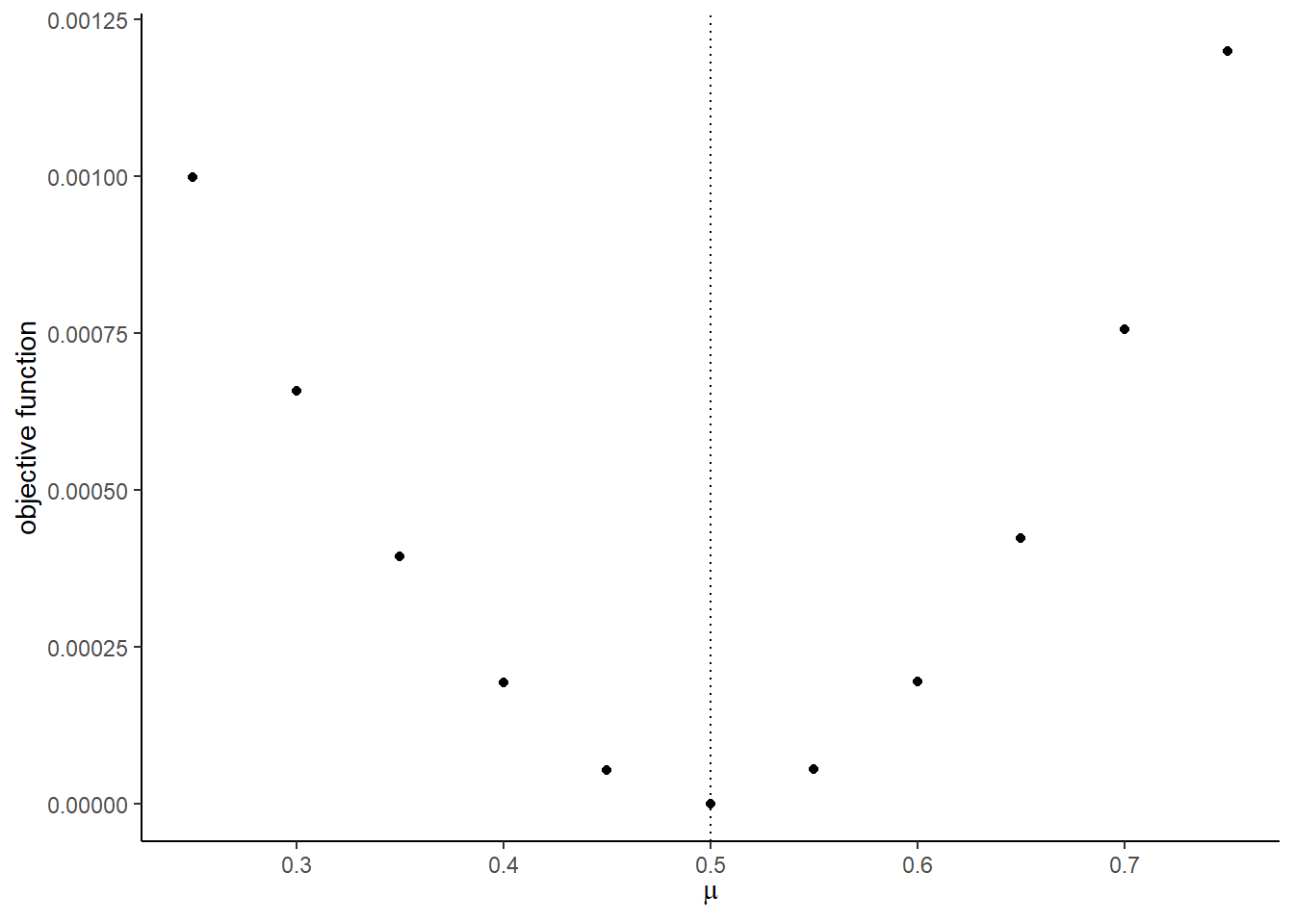

## 
## [[8]]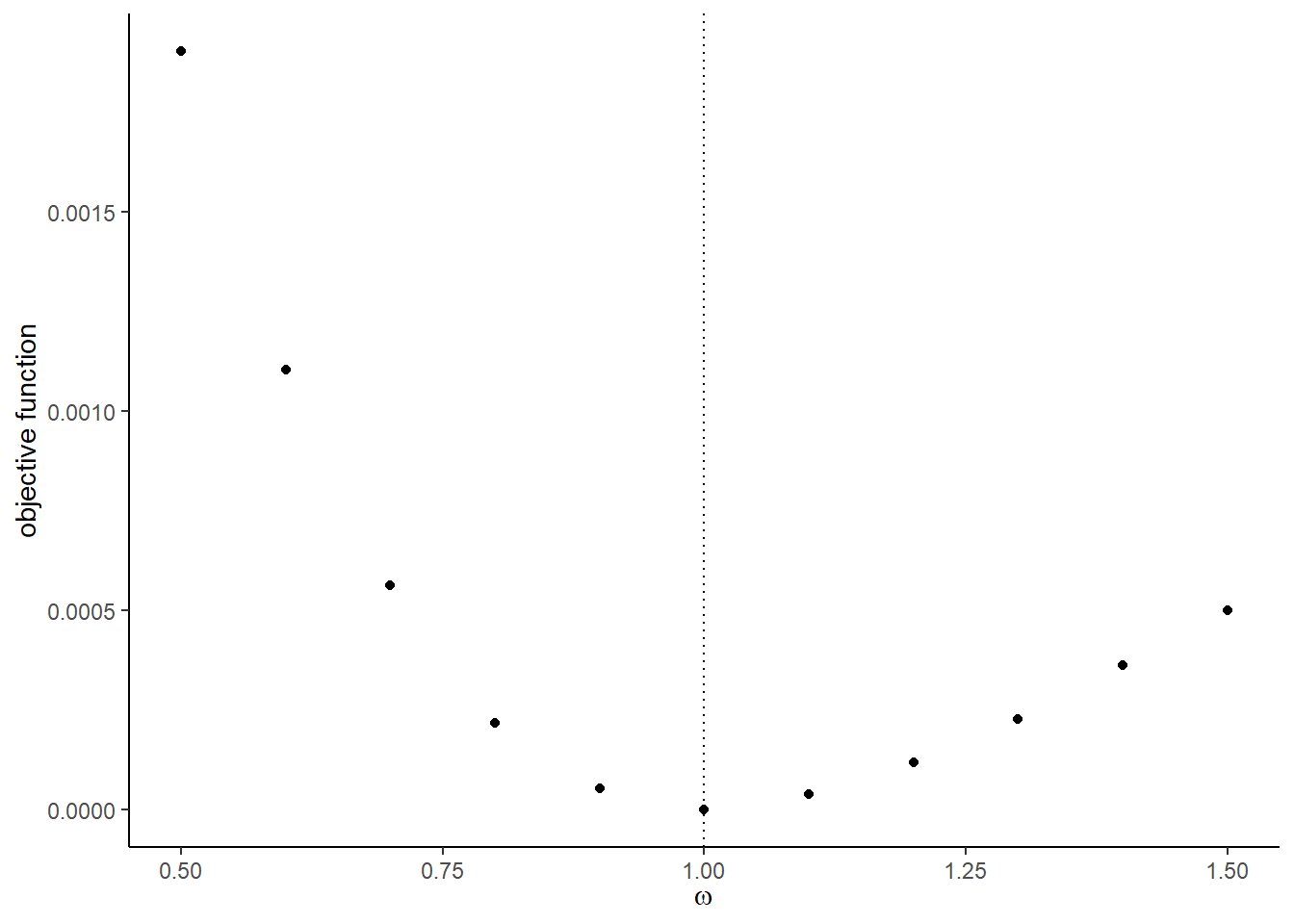

The graphs with the Monte Carlo shocks:

## [[1]]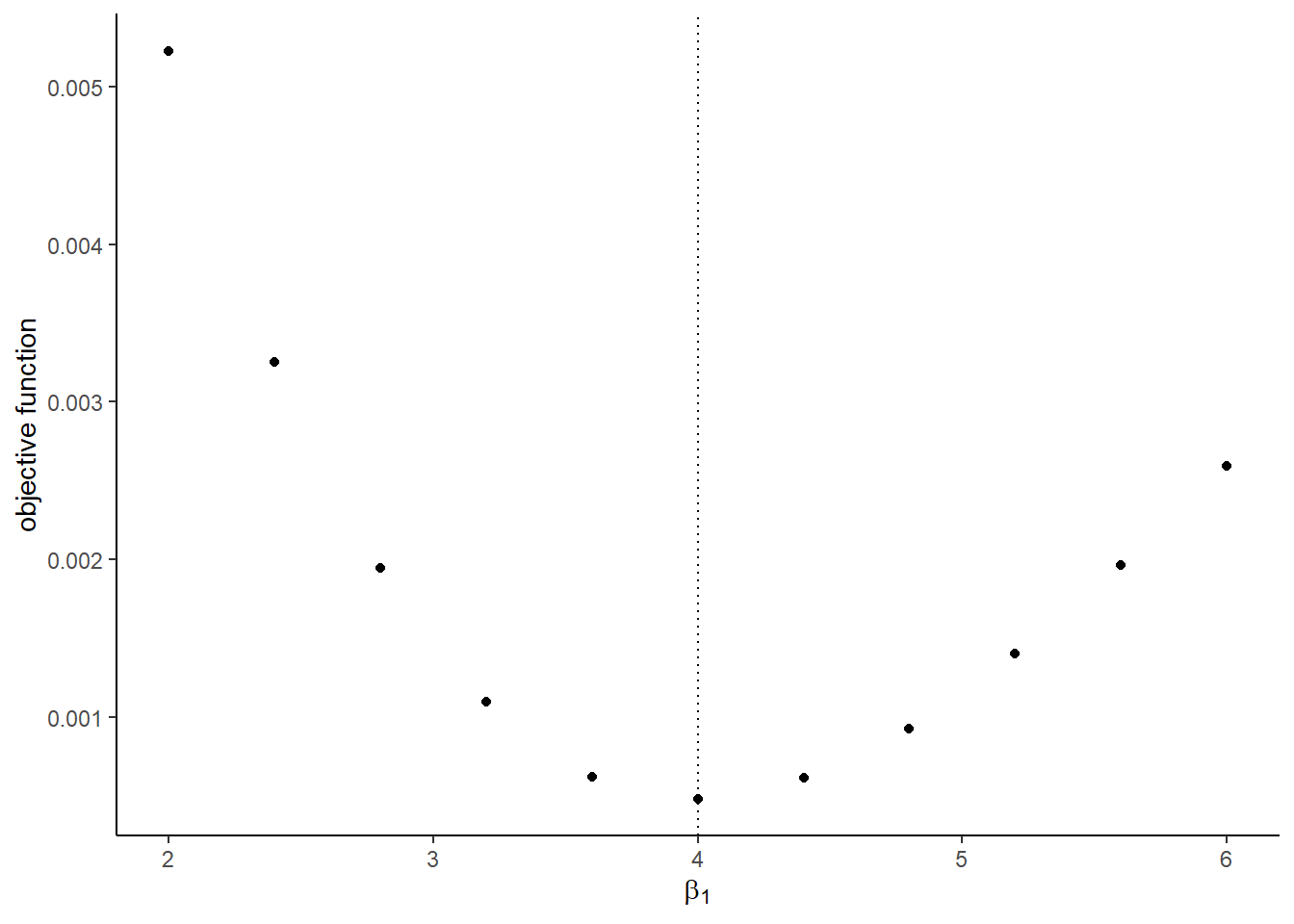

## 
## [[2]]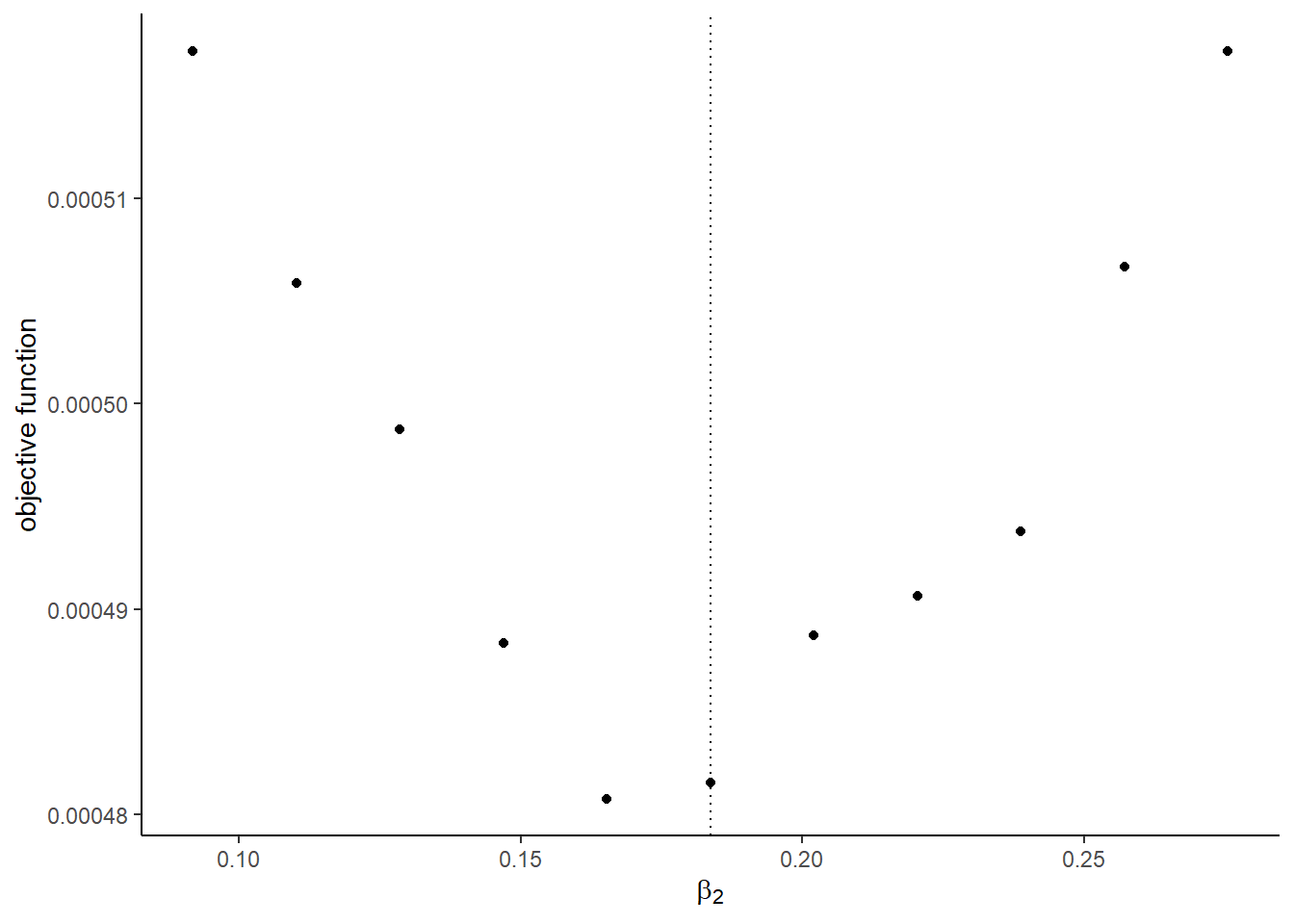

## 
## [[3]]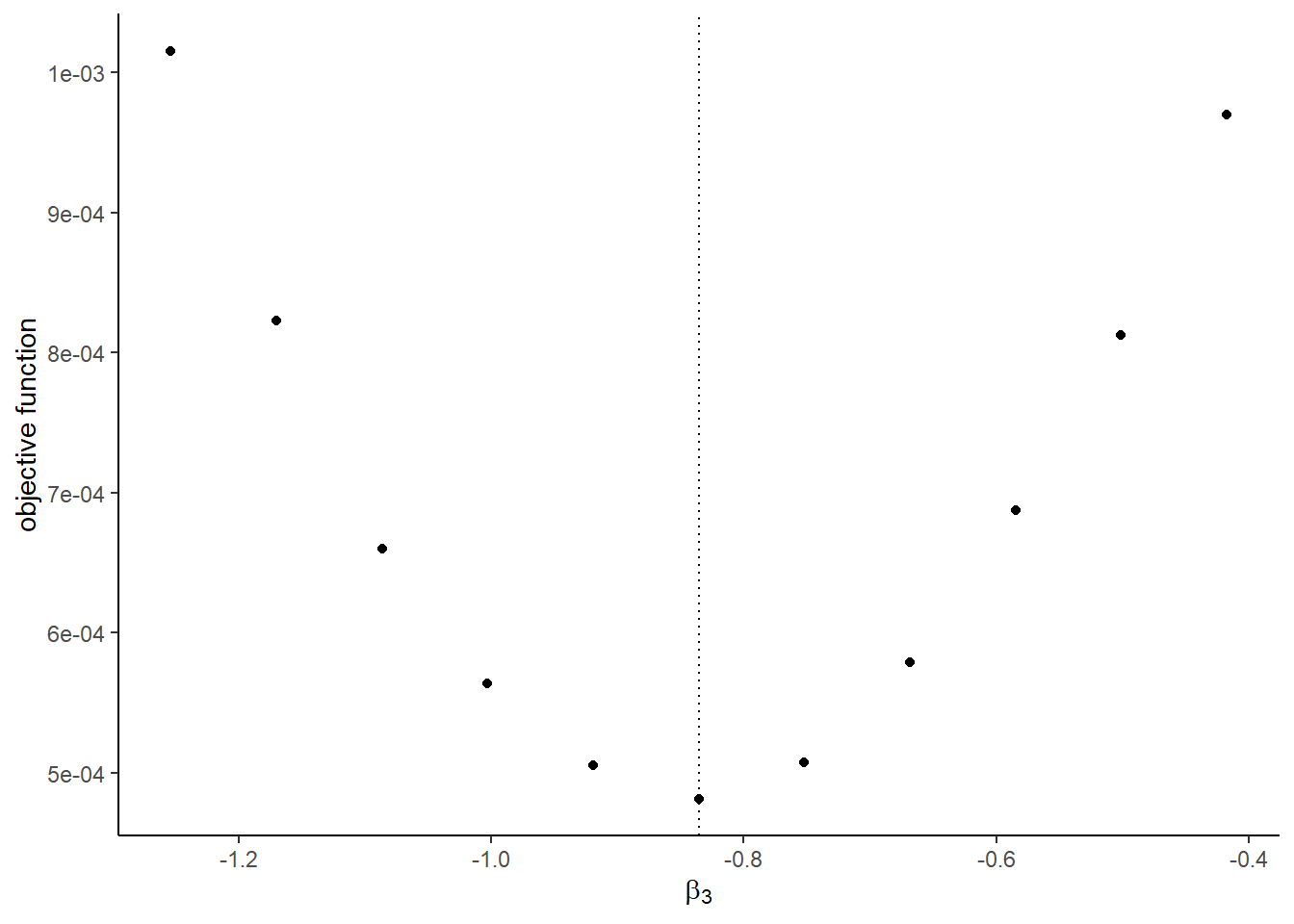

## 
## [[4]]

## 
## [[5]]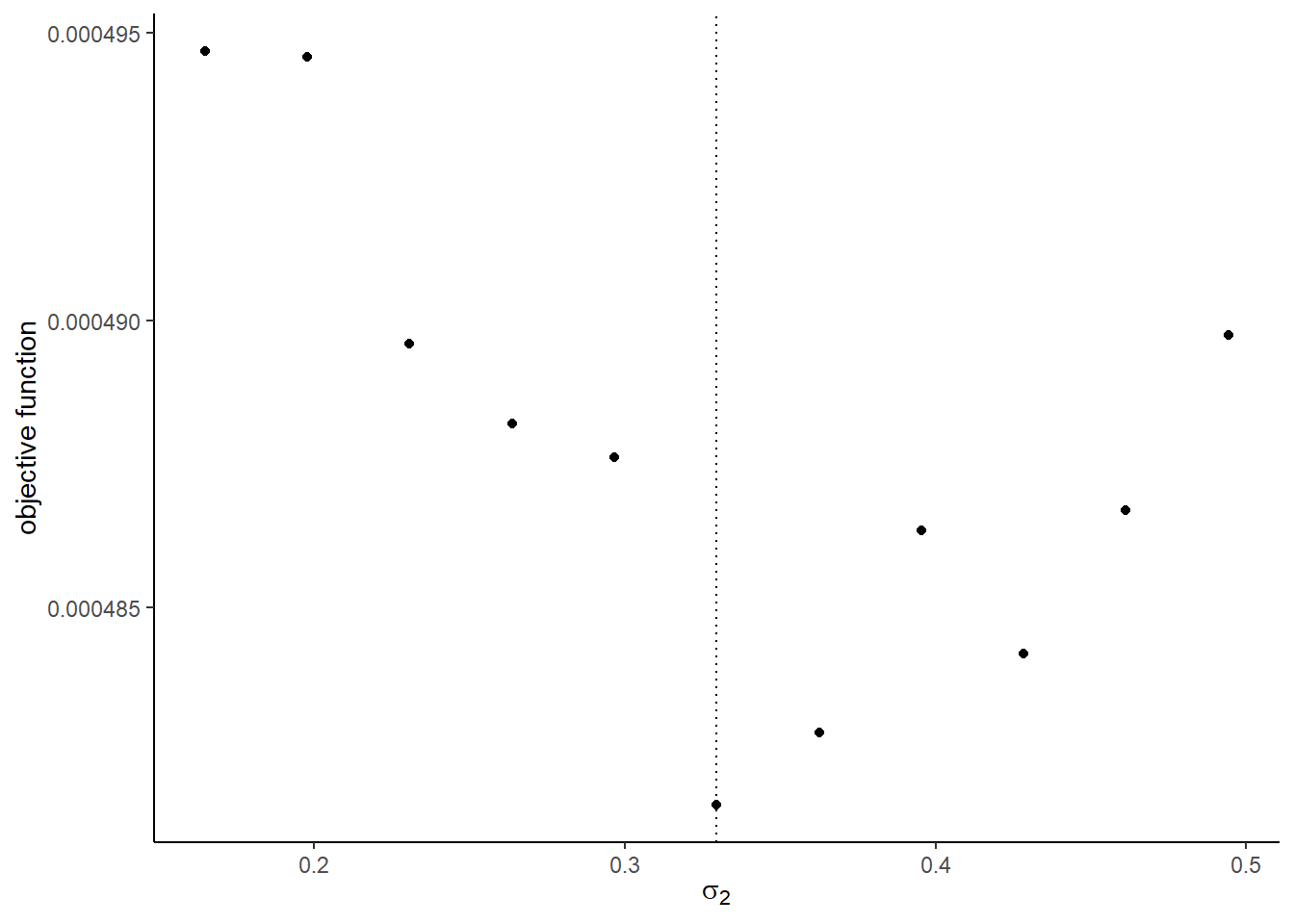

## 
## [[6]]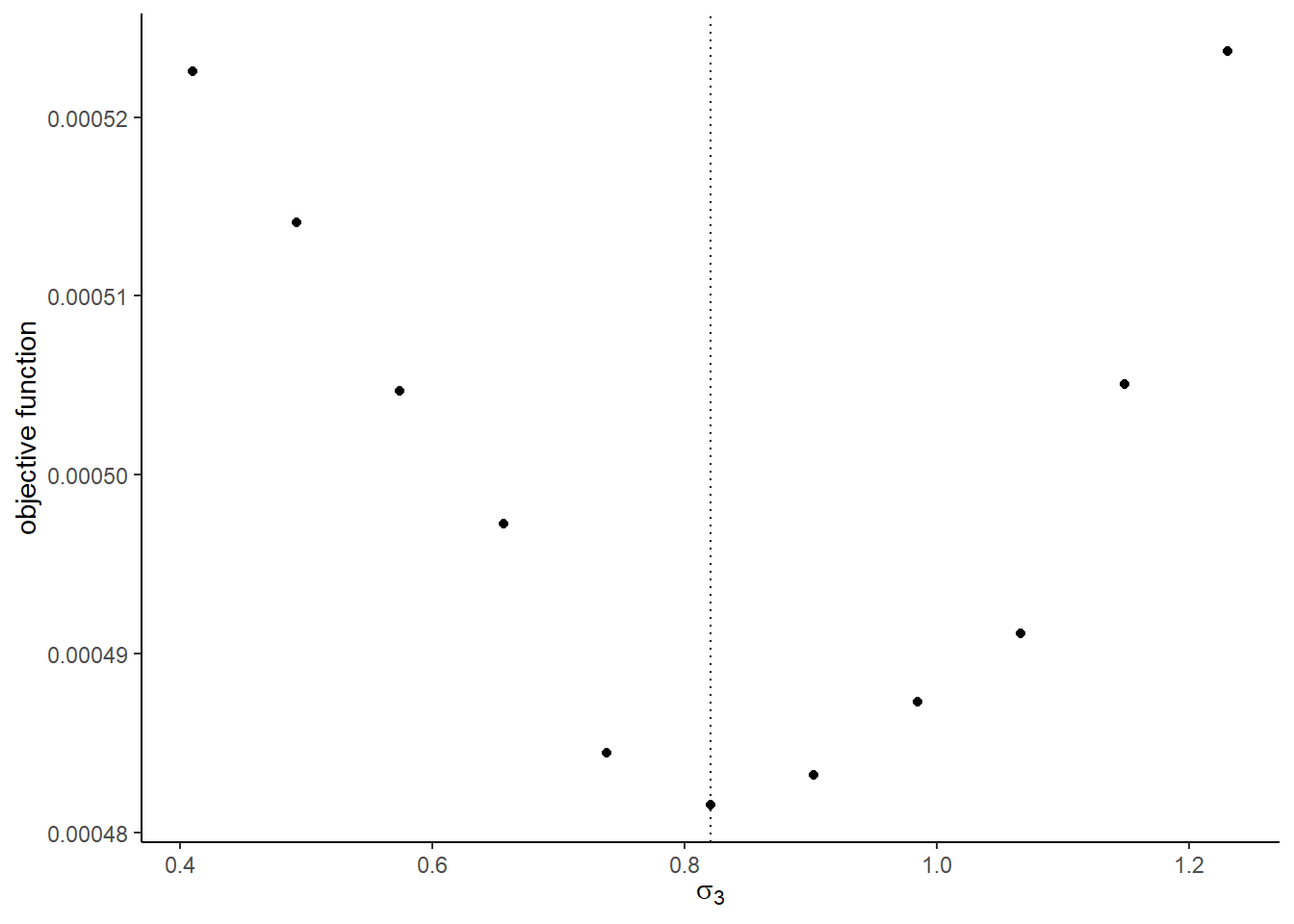

## 
## [[7]]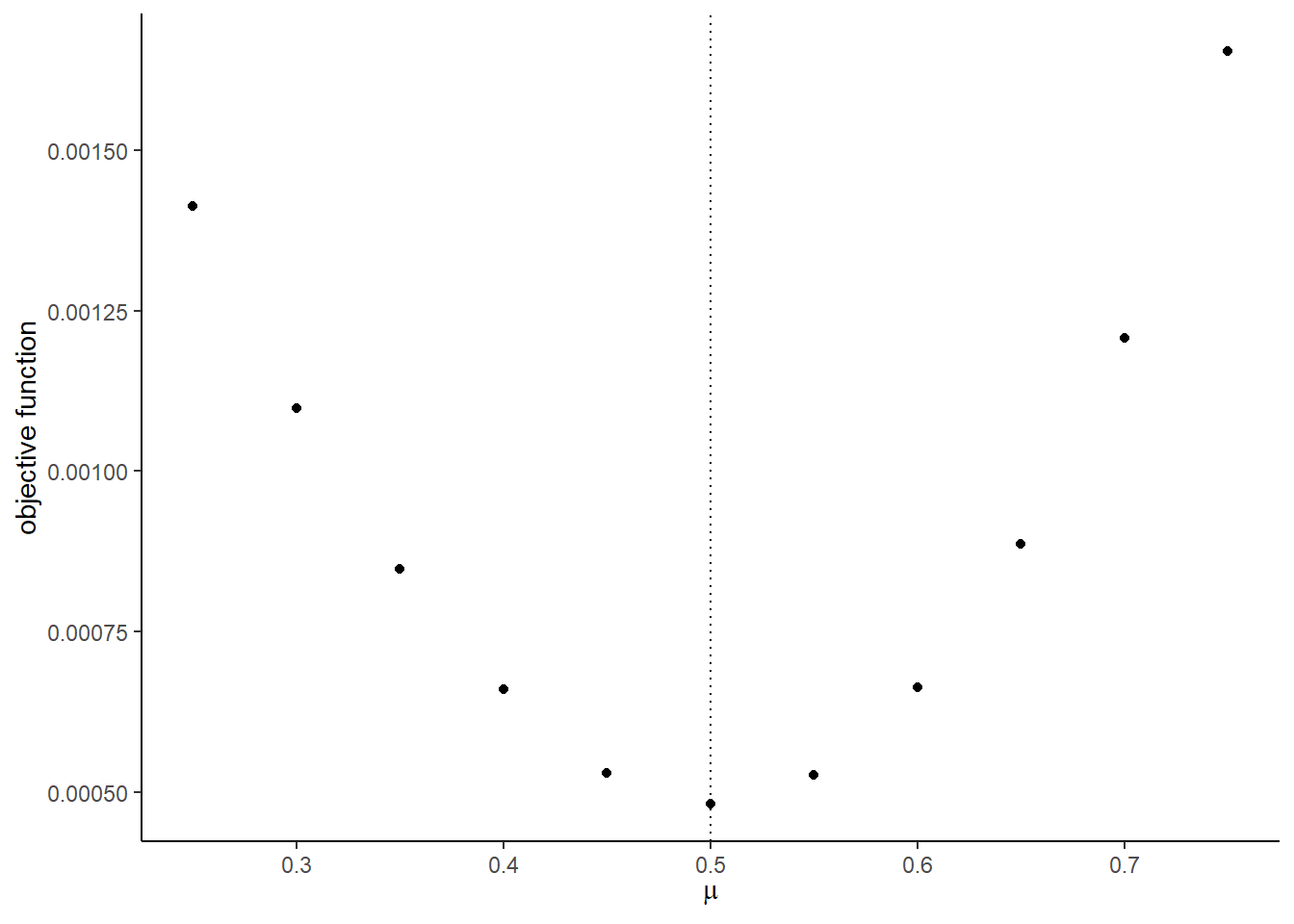

## 
## [[8]]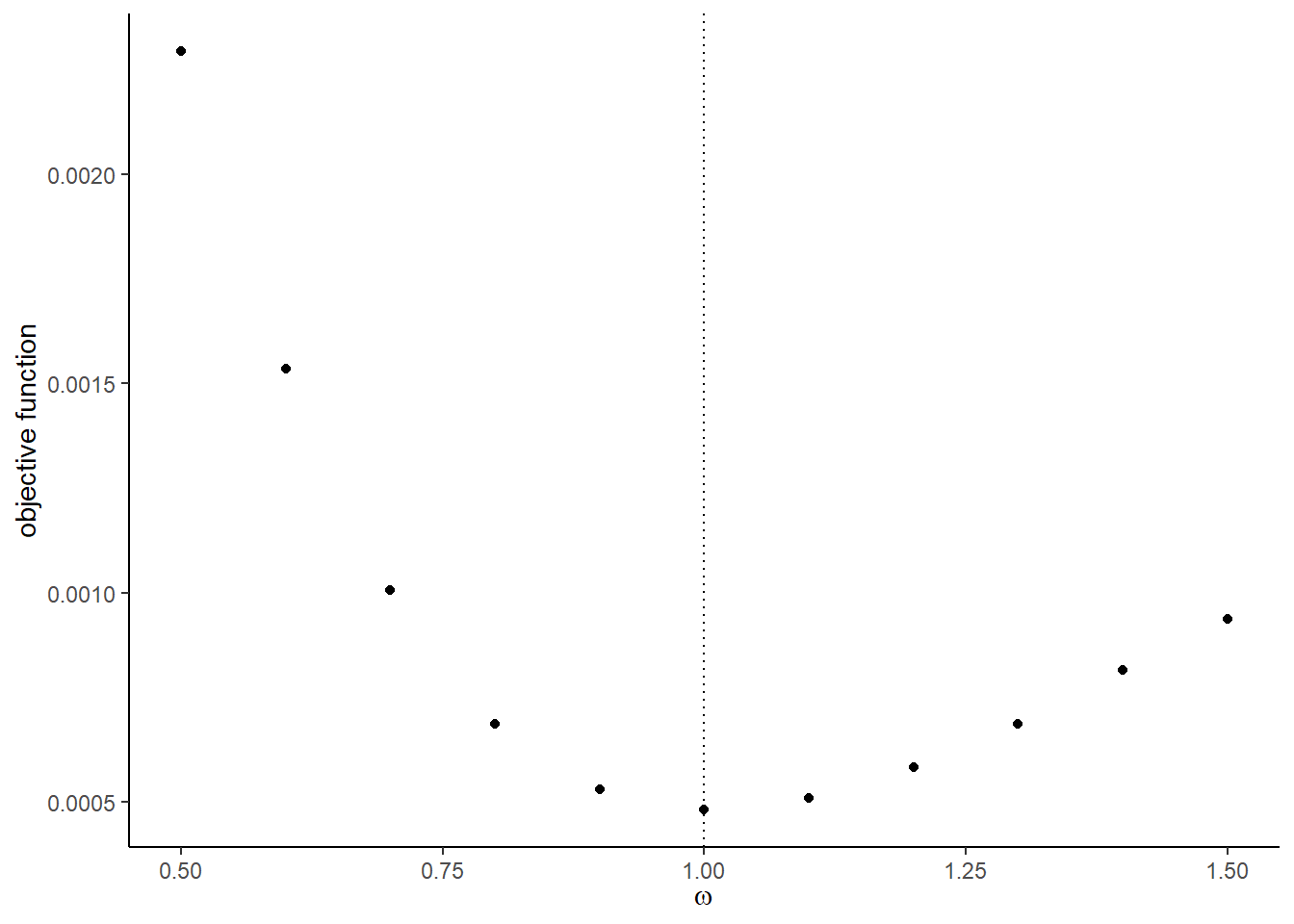

  1. Use optim to find the minimizer of the objective function using Nelder-Mead method. You can start from the true parameter values. Compare the estimates with the true parameters.
## $par
## [1]  3.9907237  0.1778582 -0.8244977  1.5326774  0.3602383  0.9336009  0.4883030
## [8]  1.0462494
## 
## $value
## [1] 0.0004678286
## 
## $counts
## function gradient 
##      237       NA 
## 
## $convergence
## [1] 0
## 
## $message
## NULL
##         true  estimates
## 1  4.0000000  3.9907237
## 2  0.1836433  0.1778582
## 3 -0.8356286 -0.8244977
## 4  1.5952808  1.5326774
## 5  0.3295078  0.3602383
## 6  0.8204684  0.9336009
## 7  0.5000000  0.4883030
## 8  1.0000000  1.0462494