Chapter 5 Merger Analysis

5.1 Motivations

  • Measuring the market power of firms and predicting the possible consequence of horizontal merger cases is one of the primary goal of empirical industrial organization.
  • This is important for antitrust authority to review merger cases.
  • To do so, we integrate the product/cost function estimation and demand function estimation techniques.
  • We introduce the last piece of parameters that characterize the market competition, conduct parameter, and discuss its identification.
  • Then, we conduct the first kind of counterfactual analysis, the merger simularion.
  • In this exercise, we predict the market response when the ownership structure of product is changed due to a hypothetical merger.
  • Every market institution needs its own model for merger simulation:
  • Gowrisankaran, Nevo, & Town (2015):
    • In the U.S. hospitals and managed care organizations (MGO) negotiate the hospital prices and the coinsurance rates.
    • What if hospitals are merged? How much do the hospital prices and the coinsurance rates increase?
  • Smith (2004):
    • Sometimes the same service is sold through multiple stores such as in the supermarket industry.
    • How does this multi-store nature affect the merger effects?
  • Ivaldi & Verboven (2005) reviews the cases in the European Commission.

5.2 Identification of Conduct

5.2.1 Identification of Conduct

  • So far we have been concerned with the two types of parameters:
    • Production and/or cost function.
    • Demand function.
  • To identify the marginal cost by the revealed preference approach, we have assumed that firms are engaging in a price competition.
  • The mode of competition is another parameter of interest.
  • Can we infer the mode of competition instead of assuming it?

5.2.2 Marginal Revenue Function

  • To be specific, consider firms producing homogeneous product.
  • Under what conditions can we distinguish across Bertrand competition, Cournot competition, and collusion? (Timothy F. Bresnahan, 1982).
  • Consider the following marginal revenue function: \[\begin{equation} MR(Q) \equiv \lambda Q P'(Q) + P(Q), \end{equation}\] where \(Q\) is the aggregate quantity, \(P(Q)\) is the inverse demand function.
  • This formula nests Bertrand, Cournot, and collusion:
  • Bertrand:
    • In Bertrand, a firm cannot change the market price.
    • If a firm increases the production by one unit, whose revenue increases by \(P(Q)\).
    • Therefore, \(\lambda = 0\).
  • Cournot:
    • In Cournot, the marginal revenue of firm \(f\) is: \[ q_f P'(Q) + P(Q). \]
    • Therefore, \(\lambda = s_f\), the quantity share of the firm \(f\).
  • Collusion:
    • Under collusion, firms behave like a single monopoly.
    • Then, the marginal revenue is: \[ QP'(Q) + P(Q). \]
    • Therefore, \(\lambda = 1\).
  • The identification of the mode of competition in this context is equivalent to the identification of \(\lambda\), the conduct parameter.

5.2.3 First-Order Condition

  • Let \(MC(q_f)\) be the marginal cost of firm \(f\).
  • Given the previous general marginal revenue function, the first-order condition for profit maximization for firm \(f\) is written as: \[\begin{equation} \lambda Q P'(Q) + P(Q) = MC(q_f). \end{equation}\]
  • The system of equations for \(f = 1, \cdots, F\) determine the market equilibrium.

5.2.4 Linear Model

  • To be simple, consider a linear inverse demand function: \[\begin{equation} P^D(Q) = \frac{\alpha_0}{\alpha_1} + \frac{1}{\alpha_1}Q + \frac{\alpha_2}{\alpha_1} X + \frac{1}{\alpha_1}u^D, \end{equation}\] where \(X_t\) is a vector of observed demand sifters.
  • Consider a linear marginal cost function: \[\begin{equation} MC(q_{f}) = \beta_0 + \beta_1 q_{f} + \beta_2 W + u^S, \end{equation}\] where \(W\) is a vector of observed cost sifters.

5.2.5 Pricing Equation

  • Inserting the inverse demand function and marginal cost function to the optimality condition: \[\begin{equation} \frac{\lambda}{\alpha_1} Q + P^S(Q) = \beta_0 + \beta_1 q_f + \beta_2 W + u^S \end{equation}\]
  • Summing them up and dividing by the number of firms \(N\): \[\begin{equation} \frac{\lambda}{\alpha_1} Q + P^S(Q) = \beta_0 + \frac{\beta_1}{N} Q + \beta_2 W_t + u^S, \end{equation}\]
  • This determines the aggregate pricing equation: \[\begin{equation} \begin{split} P^S(Q) &= \beta_0 + (\frac{\beta_1}{N} - \frac{\lambda}{\alpha_1})Q + \beta_2 W + u^S\\ &= \beta_0 + \gamma Q + \beta_2 W + u^S. \end{split} \end{equation}\]
  • The key parameter is: \[\begin{equation} \gamma \equiv \frac{\beta_1}{N} - \frac{\lambda}{\alpha_1}. \end{equation}\]

5.2.6 Identification of Inverse Demand Function and Pricing Equation

  • We have two systems of reduced-form equations: \[\begin{equation} \begin{split} &P^D(Q) = \frac{\alpha_0}{\alpha_1} + \frac{1}{\alpha_1}Q + \frac{\alpha_2}{\alpha_1} X + \frac{1}{\alpha_1}u^D,\\ &P^S(Q) = \beta_0 + \gamma Q + \beta_2 W + u^S. \end{split} \end{equation}\]
  • If we observe a demand shifter \(X\), then it can be used as an instrument for \(Q\) in the pricing equation to identify the parameters in the pricing equation.
  • If we observe a cost shifter \(W_t\), then it can be used as an instrument for \(Q\) in the inverse demand function to identify the parameters in the pricing equation.
  • Thus, we can identify the reduced-form parameters \((\alpha_0, \alpha_1, \alpha_2)\) and \((\beta_0, \gamma, \beta_2)\) if we observe a demand shifter \(X\) and a cost shifter \(W\).
  • However, this is not enough to separately identify the structural-form parameters \(\beta_1\) and \(\lambda\) in \(\gamma\).

5.2.7 The Conduct Parameter is Unidentified

  • Even if the demand function and pricing equation (supply function) are identified, we still cannot identify the conduct parameter \(\lambda\).
  • The price at a quantity may be high either because of the high marginal cost or because of the high markup.
  • Remember that the identification of \(\gamma\) and \(\alpha_1\) do not determine the value of \(\lambda\) and \(\beta_1\) in: \[\begin{equation} \gamma = \frac{\beta_1}{N} - \frac{\lambda}{\alpha_1}. \end{equation}\]
  • \(\beta_1\) is the derivative of the marginal cost.
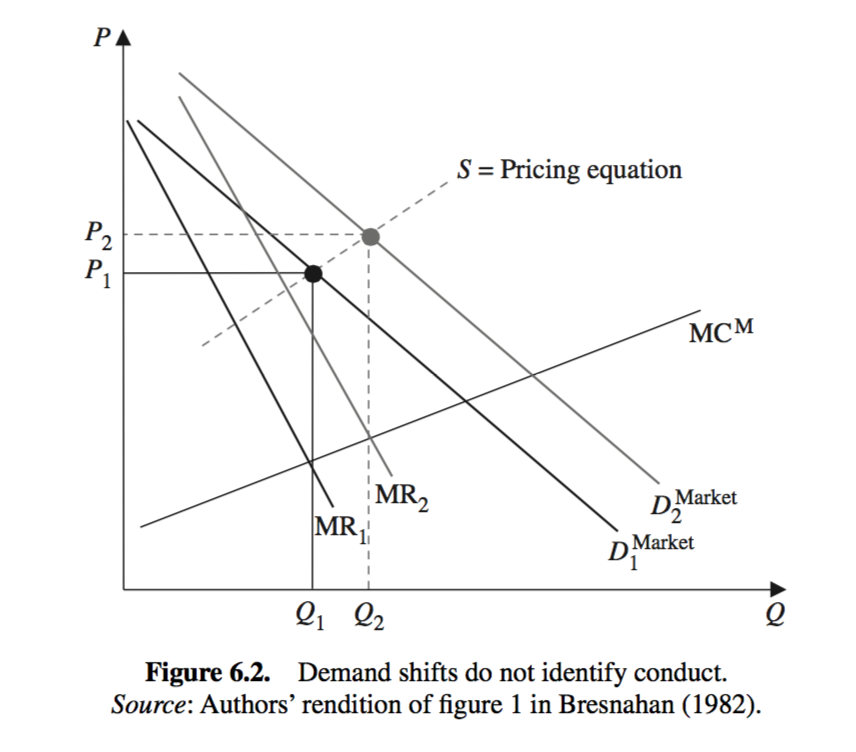
Figure 6.2 of Davis (2006)

Figure 5.1: Figure 6.2 of Davis (2006)

5.2.8 Identification of the Conduct Parameter: When Cost Data is Available

  • If there is reliable cost data, we can directly identify the marginal cost function: \[\begin{equation} MC(q_f) = \beta_0 + \beta_1 q_f + \beta_2 W + u^S, \end{equation}\] and so \(\beta_1\).
  • Then, in a combination with the identification of inverse demand function and pricing equation, \(\lambda\) is identified as: \[\begin{equation} \lambda = \alpha_1 \left(\frac{\beta_1}{N} - \gamma\right). \end{equation}\]

5.2.9 Identification of the Conduct Parameter: When Cost Data is Not Available

  • Remember the first-order condition: \[\begin{equation} \lambda Q P^{D\prime}(Q) + P^S(Q) = MC(q_f), \end{equation}\] where we can identify \(P^D(Q)\) and \(P^S(Q)\) if we have demand and cost shifters.
  • It is clear from this expression that we need a variation in \(P^{D\prime}(Q)\) with a fixed \(Q\) to identify \(\lambda\), i.e., something that rotates the inverse demand function.
  • Intuition: If demand becomes more elastic, prices will decrease and quantity will increase in a market with a high degree of market power.

5.2.10 Identification of the Conduct Parameter: Demand Rotater is Available

  • Let’s formalize the idea.

  • To identify the conduct parameter, we needed a demand rotater: \[\begin{equation} P^D(Q) = \frac{\alpha_0}{\alpha_1} + \frac{1}{\alpha_1}Q + \frac{\alpha_2}{\alpha_1} X + \frac{\alpha_3}{\alpha_1} Q \underbrace{Z}_{\text{demand rotater}} + \frac{1}{\alpha_1}u^D. \end{equation}\]

  • Inserting this into the first-order condition yields: \[\begin{equation} \frac{\lambda}{\alpha} Q_t (1 + \alpha Z_t)+ P^S(Q) = \beta_0 + \frac{\beta_1}{N} Q + \beta_2 W + u^s, \end{equation}\]

  • This determines the pricing equation: \[\begin{equation} \begin{split} P^S(Q) &= \beta_0 - \frac{\lambda}{\alpha_1} Q(1 + \alpha_3 Z_t) + \frac{\beta_1}{N} Q_t + \beta_2 W + u^S\\ &\equiv \beta_0 + \gamma_1 Q + \gamma_2 Z Q + \beta_2 W + u^S, \end{split} \end{equation}\] where: \[\begin{equation} \gamma_1 \equiv \frac{\beta_1}{N} - \frac{\lambda}{\alpha_1}, \gamma_2 \equiv - \frac{\lambda \alpha_3}{\alpha_1}. \end{equation}\] ### Identification of the Conduct Parameters: Demand Rotater is Available

  • If we have cost shifters \(W\), it can be used as instruments for \(Q\) in the inverse demand function to identify the demand parameters \((\alpha_0, \alpha_1, \alpha_2, \alpha_3)\).

  • If we have demand shifters \(X\), it can be used as instruments for \(Q\) in the pricing equation to identify the supply parameters \((\beta_0, \gamma_1, \gamma_2, \beta_2)\).

  • Now we can identify the reduced-form parameters \(\alpha_1, \alpha_3\) and \(\gamma_2\).

  • Then, we can not identify the conduct parameter: \[\begin{equation} \lambda = - \frac{\gamma_2 \alpha_1}{\alpha_3}. \end{equation}\]

5.2.11 Identification of Conduct in Differentiated Product Market

  • Consider the identification of conduct when there are two differentiated substitutable products and companies compete in price (Nevo, 1998).

  • Are the prices determined independently or jointly?

  • The general first-order condition is: \[\begin{equation} \begin{split} &(p_1 - c_1) \frac{\partial Q_1(p)}{\partial p_1} + Q_1^S(p) + \Delta_{12}(p_2 - c_2) \frac{\partial Q_2 (p)}{\partial p_1} = 0\\ &\Delta_{21}(p_1 - c_1)\frac{\partial Q_1(p)}{\partial p_2} + Q_2^S(p) + (p_2 - c_2) \frac{\partial Q_2 (p)}{\partial p_2} = 0, \end{split} \end{equation}\] where

  • \(\Delta_{12} = \Delta_{21} = 0\) if prices are determined independently.

  • \(\Delta_{12} = \Delta_{21} = 1\) if price are determined jointly.

  • Under what conditions can we identify \(\Delta_{12}\) and \(\Delta_{21}\)?

  • We will have to rotate \(\frac{\partial Q_1(p)}{\partial p_2}\) and \(\frac{\partial Q_2 (p)}{\partial p_1}\) while keeping the other variables at the same values.

  • Miller & Weinberg (2017) infers \(\Delta\) after the MillerCoors, a joint venture of SABMiller PLC and Molson Coors Brewing, is formed.

    • The unobserved year-specific and region-specific cost shocks are identified from the outsiders and the unobserved product-specific cost shocks are assumed to be the same before and after the merger.

5.3 Merger Simulation

5.3.1 Unilateral and Coordinated Effects of a Horizontal Merger

  • There are two effects associated with a merge episode:
  1. Unilateral effect:
    • The new merged firm usually have a unilateral incentive to raise prices above their pre-merger level.
    • This unilateral effect may lead to the other firms to have an unilateral incentive to raise price, and the reaction continues to reach the new equilibrium.
    • The latter chain reaction is sometimes called the multi-lateral effect.
    • In economic theory, it is the price change when the same mode of competition (say, the Bertrand-Nash equilibrium) is played.
    • \(\Delta\) is either 0 or 1: firms internalize the profits from owned product but do not internalize the other products.
  2. Coordinated effect:
    • After the merger, the mode of competition may change.
    • For example, the tacit collusion becomes easier and it can happen.
    • This effect, caused by the change in the mode of competition, is called the coordinated effect of a merger.
    • In this case, the conduct parameters \(\Delta\) may take positive values for products owned by the rival firms.

5.3.2 Merger Simulation

  • In merger simulation, we compute the equilibrium under different ownership structure.
  • This amounts to run a counterfactual simulation hypothetically changing the conduct parameter \(\Delta\).
  • The idea stems back to Farrell & Shapiro (1990), Werden & Frobe (1993), Hausman et al. (1994).
  • Before running the simulation, you have to be very careful about the model assumptions:
    • In music industry, firms compete not in price but in advertisement.
    • If technological diffusion is important, firms may set dynamic pricing.
  • This is the first counterfactual analysis we study in this lecture.
  • The results are valid only if the modeling assumptions are correct.

5.3.3 Quantifying the Unilateral Effect

  • See Nevo (2000) and Nevo (2001).
  • There are \(J\) products, \(\mathcal{J} = \{1, \cdots, J\}\).
  • We can have multiple markets but we suppress the market index.
  • Firm \(f\) produces a set of products which we denote \(\mathcal{J}_f \subset \mathcal{J}\).
  • Let \(mc_j\) be the constant marginal cost of producing good \(j\).
  • Thus assuming a separable cost function.
    • We can relax this assumption for the estimation.
    • However, once you admit that the costs can be non-separable, you will start to wonder what happens to the cost function if two firms merged and started to produce the two products that were previously produced by separate firms.
  • Let \(D_j(p)\) be the demand for product \(j\) when the price vector is \(p\).
  • The problem for firm \(f\) given the price of other firms \(p_{-f}\) is: \[\begin{equation} \max_{p_f} \sum_{j \in \mathcal{J}_f} \Pi_j(p_f, p_{-f}) = \sum_{j \in \mathcal{J}_f} (p_j - mc_j) D_j(p_f, p_{-f}), \end{equation}\] where \(p_f = \{p_j\}_{j \in \mathcal{J}_f}\), \(p_{-f} = \{p_j\}_{j \in \mathcal{J} \setminus \mathcal{J}_f}\).

5.3.4 Pre-Merger Equilibrium

  • The first-order condition for firm \(f\) is: \[\begin{equation} D_k(p) + \sum_{j \in \mathcal{J}_f} (p_j - mc_j) \frac{\partial D_j(p)}{\partial p_k} = 0, \forall k \in \mathcal{J}_f. \end{equation}\]
  • Let \(\Delta_{jk}^{pre}\) takes 1 if same firm produces \(j\) and \(k\) and 0 otherwise before the merger.
  • The first-order condition can be written as: \[\begin{equation} D_k(p) + \sum_{j \in \mathcal{J}} \Delta_{jk}^{pre}(p_j - mc_j) \frac{\partial D_j(p)}{\partial p_k} = 0, \forall k \in \mathcal{J}_f. \end{equation}\]
  • In terms of the product share: \[\begin{equation} s_k(p) + \sum_{j \in \mathcal{J}} \Delta_{jk}^{pre}(p_j - mc_j) \frac{\partial s_j(p)}{\partial p_k} = 0, \forall k \in \mathcal{J}_f. \end{equation}\]
  • Let \(\Delta^{pre}\) be a \(J \times J\) matrix whose \((j, k)\)-element is \(\Delta_{jk}\).
  • At the end of the day, performing a merger simulation is to recompute the equilibrium with different ownership structure encoded in \(\Delta\).

5.3.5 Post-Merger Equilibrium

  • Let \(\Omega^{pre}(p)\) is a matrix whose \((j, k)\)-element is:

\[\begin{equation} - \frac{\partial s_{j}(p)}{\partial p_k} \Delta_{jk}^{pre}. \end{equation}\]

  • Then, by the first-order condition, the marginal cost should be: \[\begin{equation} mc = p - \Omega^{pre}(p)^{-1} s(p). \end{equation}\]

  • If the ownership structure \(\Delta^{pre}\) is changed to \(\Delta^{post}\), and \(\Omega^{pre}\) changed to \(\Omega^{post}\), the post-merger price is determined by solving the non-linear equation: \[\begin{equation} p^{post} = mc + \Omega^{post}(p^{post})^{-1}s(p^{post}). \end{equation}\]

  • The post-merger share is given by: \[\begin{equation} s^{post} = s(p^{post}). \end{equation}\]

5.3.6 Consumer Surplus

  • Suppose that the demand function is based on the mixed-logit model such that the indirect utility is: \[\begin{equation} u_{ijt} = x_{jt} \beta_i + \alpha_i p_{jt} + \xi_{j} + \xi_t + \Delta \xi_{jt} + \epsilon_{ijt}, \end{equation}\] with \(\epsilon_{ijt}\) is drawn from i.i.d. Type-I extreme value distribution and the consumer-level heterogeneity:

\[\begin{equation} \begin{pmatrix} \alpha_i \\ \beta_i \end{pmatrix} = \begin{pmatrix} \alpha\\ \beta \end{pmatrix} + \Pi z_i + \Sigma \nu_i, \nu_i \sim N(0, I_{K + 1}). \end{equation}\]

  • Then, the compensated variation due to the price change for consumer \(i\) is: \[\begin{equation} CV_{it} = \frac{\ln (\sum_{j = 0}^J \exp(V_{ijt}^{post}) ) - \ln (\sum_{j = 0}^J \exp(V_{ijt}^{pre})) }{\alpha_i}, \end{equation}\] where \(V_{ijt}^{post}\) and \(V_{ijt}^{pre}\) are indirect utility for consumer \(i\) to purchase good \(j\) at the prices after and before the merger.
  • This formula holds only if the price enters linearly in the indirect utility (no income effect).
  • For general case, see Small & Rosen (1981) and D. Mcfadden et al. (1995).

5.3.7 Quantifying the Coordinated Effect

  • The repeated-game theory suggests that a collusion is sustainable if and only if it it incentive compatible: the collusion profit is no less than the deviation profit for each member of the collusion.
  • The theory provides a check list that affects the incentive compatibility such as the market share, cost asymmetry, and demand dynamics.
  • But it is often hard to judge the coordinated effects from these qualitative information, because mergers simultaneously change many factors and the factors may encourage or hinder collusion.
  • Miller & Weinberg (2017) retrospectively studies the coordinated effect of a merger.
  • Is prospective analysis of coordinated effects possible as well as the analysis of unilateral effects?
  • If we can identify the demand and cost functions, we can calculate the collusion profits and deviation profits.
  • If we specify the collusion strategy, we can write down the incentive compatibility.
  • We can check how the incentive compatibility change when a hypothetical merger happens.
  • The problem is the identification of conduct: to identify the cost function, we need to know the conduct.
  • Thus, the stated strategy will work only if we have a data during which we are sure that there was no collusion, or there was a particular type of collusion.
  • Igami & Sugaya (2018) use the detailed information of vitamin C cartel case and apply this approach.

References

Bresnahan, Timothy F. (1982). The oligopoly solution concept is identified. Economics Letters, 10(1-2), 87–92.
Farrell, J., & Shapiro, C. (1990). American Economic Association Horizontal Mergers: An Equilibrium Analysis. Source: The American Economic Review, 80(1), 107–126.
Gowrisankaran, G., Nevo, A., & Town, R. (2015). Mergers When Prices Are Negotiated: Evidence from the Hospital Industry. American Economic Review, 105(1), 172–203.
Hausman, Leonard, & Zona. (1994). Competitive Analysis with Differenciated Products. Annales d’Économie et de Statistique, (34), 159–180.
Igami, M., & Sugaya, T. (2018). Measuring the Incentive to Collude: The Vitamin Cartels, 1990-1999.
Ivaldi, M., & Verboven, F. (2005). Quantifying the effects from horizontal mergers in European competition policy. International Journal of Industrial Organization, 23(9-10), 669–691.
Mcfadden, D., Geweke, J., Hajivassiliou, V., Johnson, R., Lancaster, T., Rossi, P., … Waters, S. (1995). Computing Willingness-to-pay in Random Utility Models.
Miller, N. H., & Weinberg, M. C. (2017). Understanding the Price Effects of the MillerCoors Joint Venture. Econometrica, 85(6), 1763–1791.
Nevo, A. (1998). Identification of the Oligopoly Solution Concept in a Differentiated-Products Industry. Economics Letters, 59(3), 391–395.
Nevo, A. (2000). Mergers with differentiated products: The case of the ready-to-eat cereal industry (No. 3) (Vol. 31).
Nevo, A. (2001). Measuring Market Power in the Ready-to-Eat Cereal Industry. Econometrica, 69(2), 307–342.
Small, K. A., & Rosen, H. S. (1981). Applied Welfare Economics with Discrete Choice Models. Econometrica, 49(1), 105–130.
Smith, H. (2004). Supermarket Choice and Supermarket Competition in Market Equilibrium. Review of Economic Studies, 71(1), 235–263.
Werden, G., & Frobe, L. (1993). The Effects of Mergers in Differentiated Products Industries : Logit Demand and Merger Policy. Journal of Law, Economics, and Organization, 10, 407–426.