Chapter 16 Assignment 6: Entry and Exit Analysis

16.1 Simulate data

In this assignment, we consider a Berry-type entry model. Suppose that there are \(M\) markets indexed by \(m = 1, \cdots, M\). In each market, there are \(N_m\) potential entrants such that \(N_m \le \overline{N}\). Let \(x_m\) be the \(K\) dimensional market attributes and \(z_{im}\) be the \(L\) dimensional potential entrant attributes. The size of Monte Carlo simulations in the estimation is \(R\).

A random number generation inside %dopar% is not reproducible. Therefore, we use package doRNG to perform reproducible foreach parallel.

  1. Set the constants as follows:
registerDoParallel()
# register doRNG backend
registerDoRNG()
# set the seed
set.seed(1)
# number of markets
M <- 100
# the upper bound of the number of potential entrants
N <- 10
# the dimension of market attributes
K <- 2
# the dimension of potential entrant attributes
L <- 2
# the number of Monte Carlo simulations
R <- 100

The payoff of entrant \(i\) in market \(m\) is: \[ \pi_{im}(y_m) = x_m'\beta - \delta \ln \left(\sum_{i = 1}^{N_m} y_{im}\right) + z_{im}'\alpha + \sqrt{1 - \rho^2} \nu_{im} + \rho \epsilon_{m}, \] where \(y_{im} \in \{0, 1\}\) is the indicator for entrant \(i\) in market \(m\) to enter the market, and \(\nu_{im}\) and \(\epsilon_m\) are entrant- and market-specific idiosyncratic shocks that are drawn from an i.i.d. standard normal distribution. In each market, all the attributes and idiosyncratic shocks are observed by the potential entrants. \(N_m\), \(x_m\), \(z_{im}\), and \(y_m\) are observed to econometrician but \(\nu_{im}\) and \(\epsilon_m\) are not.

  1. Set the parameters as follows:
# parameters of interest
beta <- abs(rnorm(K)); 
beta
## [1] 0.6264538 0.1836433
alpha <- abs(rnorm(L)); 
alpha
## [1] 0.8356286 1.5952808
delta <- 1; 
delta
## [1] 1
rho <- abs(rnorm(1)); 
rho
## [1] 0.3295078
# auxiliary parameters
x_mu <- 1
x_sd <- 3
z_mu <- 0
z_sd <- 4
  1. Draw exogenous variables as follows:
# number of potential entrants
E <- 
  purrr::rdunif(
    M, 
    1, 
    N
    ); 
E
##   [1]  3  1  5  5 10  6 10  7  9  5  5  9  9  5  5  2 10  9  1  4  3  6 10 10  6  4  4
##  [28] 10  9  7  6  9  8  9  7  8  6 10  7  3 10  6  8  2  2  6  6  1  3  3  8  6  7  6
##  [55]  8  7  1  4  8  9  9  7  4  7  6  1  5  6  1  9  7  7  3  6  2 10 10  7  3  2 10
##  [82]  1 10 10  8 10  5  7  8  5  6  8  1  3 10  3  1  6  6  4
# market attributes
X <- 
  matrix(
  rnorm(
    M * K, 
    x_mu, 
    x_sd
    ),
  nrow = M
  )
colnames(X) <- paste("x", 1:K, sep = "_")
X[1:10, ]
##               x_1        x_2
##  [1,] -0.70600620 -2.6939703
##  [2,]  0.59446415  3.9516867
##  [3,]  4.53426099  1.6597744
##  [4,] -3.57070040 -3.4017501
##  [5,]  2.78183856  2.5630682
##  [6,]  1.99885111  0.5237362
##  [7,]  4.18929951  5.3937619
##  [8,]  0.08744823 -1.2982460
##  [9,]  2.11005643 -0.2906353
## [10,]  1.80129637 -1.7783285
# entrant attributes
Z <-
  foreach (
    m = 1:M
    ) %dorng% {
    Z_m <- 
      matrix(
      rnorm(
        E[m] * L, 
        z_mu, 
        z_sd
        ),
      nrow = E[m]
    )
    colnames(Z_m) <- paste("z", 1:L, sep = "_")
    return(Z_m)
  }
Z[[1]]
##             z_1       z_2
## [1,] -2.3581574 -7.334507
## [2,] -0.4604547  3.771050
## [3,]  2.7599294  4.610126
# unobserved market attributes
EP <- 
  matrix(
  rnorm(M),
  nrow = M
  )
EP[1:10, ]
##  [1] -1.1131230  0.6169665  0.5134937  0.3694591  1.7238941 -0.2061446 -1.3141951
##  [8]  0.0634741 -0.2319775  0.6350603
# unobserved entrant attributes
NU <-
  foreach (
    m = 1:M
    ) %dorng% {
    NU_m <- 
      matrix(
      rnorm(E[m]),
      nrow = E[m]
    )
    return(NU_m)
  }
NU[[1]]
##            [,1]
## [1,]  0.3934210
## [2,]  0.2303175
## [3,] -0.6046126
  1. Write a function compute_payoff(y_m, X_m, Z_m, EP_m, NU_m, beta, alpha, delta, rho) that returns the vector of payoffs of the potential entrants when the vector of entry decisions is y_m.
m <- 1
N_m <- dim(Z[[m]])[1]
y_m <- as.matrix(rep(1, N_m))
y_m[length(y_m)] <- 0
X_m <- X[m, , drop = FALSE]
Z_m <- Z[[m]]
EP_m <- EP[m, , drop = FALSE]
NU_m <- NU[[m]]


compute_payoff(
  y_m = y_m, 
  X_m = X_m, 
  Z_m = Z_m, 
  EP_m = EP_m, 
  NU_m = NU_m, 
  beta = beta, 
  alpha = alpha, 
  delta = delta, 
  rho = rho
  )
##            [,1]
## [1,] -15.296633
## [2,]   3.851629
## [3,]   0.000000
  1. Assume that the order of entry is predetermined. Assume that the potential entrants sequentially decide entry according to the order of the payoff excluding the competitive effects, i.e.: \[ x_m'\beta + z_{im}'\alpha + \sqrt{1 - \rho^2} \nu_{im} + \rho \epsilon_{m}. \] Write a function compute_order_sequential_entry(X_m, Z_m, EP_m, NU_m, beta, alpha, rho) that returns the order of entry of the potential entrants by the baseline payoff. Note that if the less profitable entrant finds it profitable to enter then the more profitable entrant still finds it profitable to enter. Then write a function compute_sequential_entry(X_m, Z_m, EP_m, NU_m, beta, alpha, delta, rho) that returns the equilibrium vector of entry at a market. To do so, you must find at which entrant the payoff becomes negative for the first time.
compute_order_sequential_entry(
    X_m = X_m,
    Z_m = Z_m, 
    EP_m = EP_m, 
    NU_m = NU_m, 
    beta = beta, 
    alpha = alpha, 
    rho = rho
    )
## [1] 3 2 1
compute_sequential_entry(
  X_m = X_m, 
  Z_m = Z_m, 
  EP_m = EP_m, 
  NU_m = NU_m, 
  beta = beta, 
  alpha = alpha, 
  delta = delta, 
  rho = rho
  )
##      [,1]
## [1,]    0
## [2,]    1
## [3,]    1
  1. Next, assume \(\rho = 0\). Assume that potential entrants simultaneously decide entry. Write a function compute_best_response_simultaneous_entry that returns the best response function of the potential participant given an entry decision. Then, write a function compute_simultaneous_entry(X_m, Z_m, EP_m, NU_m, beta, alpha, delta) that returns the equilibrium vector of entry at a market, given an initial entry decision where all firms decide to enter. To do so, you need to compute the best response given other firm’s entry decisions, and iterate the best response mapping until convergence.
compute_best_response_simultaneous_entry(
    y_m = y_m,
    X_m = X_m, 
    Z_m = Z_m, 
    EP_m = EP_m, 
    NU_m = NU_m, 
    beta = beta, 
    alpha = alpha, 
    delta = delta
    ) 
##      [,1]
## [1,]    0
## [2,]    1
## [3,]    1
compute_simultaneous_entry(
  X_m = X_m, 
  Z_m = Z_m, 
  EP_m = EP_m, 
  NU_m = NU_m, 
  beta = beta, 
  alpha = alpha,
  delta = delta
  )
##      [,1]
## [1,]    0
## [2,]    1
## [3,]    1
  1. Write a function compute_sequential_entry_across_markets(X, Z, EP, NU, beta, alpha, delta, rho) compute the equilibrium entry vectors under the assumption of sequential entry. The output should be a list of entry vectors across markets. Write a function to compute the equilibrium payoffs across markets, compute_payoff_across_markets(Y, X, Z, EP, NU, beta, alpha, delta, rho) and check that the payoffs under the equilibrium entry vectors are non-negative. Otherwise, there are some bugs in the code.
Y_sequential <-
  compute_sequential_entry_across_markets(
    X = X, 
    Z = Z, 
    EP = EP, 
    NU = NU, 
    beta = beta, 
    alpha = alpha, 
    delta = delta, 
    rho = rho
    )
Y_sequential[[1]]
##      [,1]
## [1,]    0
## [2,]    1
## [3,]    1
Y_sequential[[M]]
##      [,1]
## [1,]    1
## [2,]    1
## [3,]    1
## [4,]    0
payoff_sequential <-
  compute_payoff_across_markets(
    Y = Y_sequential, 
    X = X, 
    Z = Z, 
    EP = EP, 
    NU = NU, 
    beta = beta, 
    alpha = alpha, 
    delta = delta, 
    rho = rho
    )
min(unlist(payoff_sequential))
## [1] 0
  1. Write a function compute_simultaneous_entry_across_markets(X, Z, EP, NU, beta, alpha, delta, rho = 0) compute the equilibrium entry vectors under the assumption of simultaneous entry. The output should be a list of entry vectors across markets. Check that the payoffs under the equilibrium entry vectors are non-negative. Otherwise, there are some bugs in the code. I also recommend to write this function with
# compute simultaneous entry across markets
Y_simultaneous <-
  compute_simultaneous_entry_across_markets(
    X = X, 
    Z = Z, 
    EP = EP, 
    NU = NU, 
    beta = beta, 
    alpha = alpha, 
    delta = delta)
Y_simultaneous[[1]]
##      [,1]
## [1,]    0
## [2,]    1
## [3,]    1
Y_simultaneous[[M]]
##      [,1]
## [1,]    1
## [2,]    1
## [3,]    1
## [4,]    0
payoff_simultaneous <-
  compute_payoff_across_markets(
    Y = Y_simultaneous, 
    X = X, 
    Z = Z, 
    EP = EP, 
    NU = NU, 
    beta = beta, 
    alpha = alpha, 
    delta = delta, 
    rho = 0
    )
min(unlist(payoff_simultaneous))
## [1] 0

16.2 Estimate the parameters

We estimate the parameters by matching the actual and predicted number of entrants in each market. To do so, we simulate the model for \(R\) times. Under the assumption of the sequential entry, we can uniquely predict the equilibrium identify of the entrants. So, we consider the following objective function: \[ \frac{1}{RM}\sum_{r = 1}^R \sum_{m = 1}^M \left[\sum_{i = 1}^{N_m}|y_{im} - y_{im}^{(r)}| \right]^2, \] where \(y_{im}^{(r)}\) is the entry decision in \(r\)-th simulation. On the other hand, under the assumption of the simultaneous entry, we can only uniquely predict the equilibrium number of the entrants. So, we consider the following objective function: \[ \frac{1}{RM}\sum_{r = 1}^R \sum_{m = 1}^M \left[\sum_{i = 1}^{N_m}(y_{im} - y_{im}^{(r)}) \right]^2, \]

  1. Draw \(R\) unobserved shocks:
 set.seed(1)
# unobserved market attributes
EP_mc <-
  foreach (
    r = 1:R
    ) %dorng% {
    EP <- 
      matrix(
      rnorm(M),
      nrow = M
      )
    return(EP)
  }


head(EP_mc[[1]])
##             [,1]
## [1,]  0.74570967
## [2,] -0.07155828
## [3,] -0.03724045
## [4,]  0.69069075
## [5,] -0.71328829
## [6,]  0.01630815
# unobserved entrant attributes
NU_mc <-
  foreach (
    r = 1:R
    ) %dorng% {
  NU <-
    foreach (
      m = 1:M
      ) %do% {
      NU_m <- 
        matrix(
        rnorm(E[m]),
        nrow = E[m]
        )
      return(NU_m)
    }
  return(NU)
  }

NU_mc[[1]][[1]]
##            [,1]
## [1,]  0.2226442
## [2,] -1.1481303
## [3,] -0.1690491
  1. Write a function compute_monte_carlo_sequential_entry(X, Z, EP_mc, NU_mc, beta, alpha, delta, rho) that returns the Monte Carlo simulation. Then, write function compute_objective_sequential_entry(Y, X, Z, EP_mc, NU_mc, theta) that callscompute_monte_carlo_sequential_entry and returns the value of the objective function given data and parameters under the assumption of sequential entry.
# sequential entry
theta <- 
  theta_sequential <-
  c(
    beta, 
    alpha, 
    delta, 
    rho
    )
Y <- Y_sequential
# compute monte carlo simulations 
Y_mc <- 
  compute_monte_carlo_sequential_entry(
    X = X, 
    Z = Z, 
    EP_mc = EP_mc, 
    NU_mc = NU_mc, 
    beta = beta, 
    alpha = alpha, 
    delta = delta, 
    rho = rho
    )
Y_mc[[1]][[1]]
##      [,1]
## [1,]    0
## [2,]    1
## [3,]    1
# compute objective function
compute_objective_sequential_entry(
  Y = Y, 
  X = X, 
  Z = Z, 
  EP_mc = EP_mc, 
  NU_mc = NU_mc, 
  theta = theta
  )
## [1] 0.34
  1. Write a function compute_objective_simultaneous_entry(Y, X, Z, EP_mc, NU_mc, theta) that returns the value of the objective function given data and parameters under the assumption of simultaneous entry.
# simultaneous entry
theta <- 
  theta_simultaneous <-
  c(
    beta, 
    alpha, 
    delta
    )
Y <- Y_simultaneous
# compute monte carlo simulations
Y_mc <- 
  compute_monte_carlo_simultaneous_entry(
  X = X, 
  Z = Z, 
  EP_mc = EP_mc, 
  NU_mc = NU_mc, 
  beta = beta, 
  alpha = alpha, 
  delta = delta
  )
Y_mc[[1]][[1]]
##      [,1]
## [1,]    0
## [2,]    1
## [3,]    1
# compute objective function
compute_objective_simultaneous_entry(
  Y = Y, 
  X = X, 
  Z = Z, 
  EP_mc = EP_mc, 
  NU_mc = NU_mc, 
  theta = theta
  )
## [1] 0.2456
  1. Check the value of the objective function around the true parameter under the assumption of the sequential entry.
# sequential entry
theta <- 
  theta_sequential <-
  c(
    beta, 
    alpha, 
    delta, 
    rho
    )
Y <- Y_sequential
model <- compute_sequential_entry_across_markets
label <- c(
           paste("\\beta_", 1:K, sep = ""), 
           paste("\\alpha_", 1:L, sep = ""),
           "\\delta",
           "\\rho"
           )
label <- paste("$", label, "$", sep = "")
# compute the graph
graph <- 
  foreach (
    i = 1:length(theta)
    ) %do% {
  theta_i <- theta[i]
  theta_i_list <- theta_i * seq(0.5, 1.5, by = 0.1)
  objective_i <- 
    foreach (
              j = 1:length(theta_i_list),
             .combine = "rbind"
             ) %do% {
               theta_ij <- theta_i_list[j]
               theta_j <- theta
               theta_j[i] <- theta_ij
               objective_ij <- 
                 compute_objective_sequential_entry(
                   Y, 
                   X, 
                   Z, 
                   EP_mc, 
                   NU_mc, 
                   theta_j
                   )
               return(objective_ij)
             }
  df_graph <- 
    data.frame(
      x = theta_i_list, 
      y = objective_i
      ) 
  g <- 
    ggplot(
      data = df_graph, 
      aes(
        x = x, 
        y = y
        )
      ) + 
    geom_point() +
    geom_vline(
      xintercept = theta_i, 
      linetype = "dotted"
      ) +
    ylab("objective function") + 
    xlab(TeX(label[i])) + 
    theme_classic()
  return(g)
}
saveRDS(
  graph, 
  file = "data/a6/A6_graph_sequential.rds"
  )
graph <- readRDS(file = "data/a6/A6_graph_sequential.rds")
graph
## [[1]]

## 
## [[2]]

## 
## [[3]]

## 
## [[4]]

## 
## [[5]]

## 
## [[6]]

  1. Check the value of the objective function around the true parameter under the assumption of the simultaneous entry.
# simultaneous entry
theta <- 
  theta_simultaneous <-
  c(
    beta, 
    alpha, 
    delta
    )
Y <- Y_simultaneous
model <- compute_simultaneous_entry_across_markets
label <- c(
           paste("\\beta_", 1:K, sep = ""), 
           paste("\\alpha_", 1:L, sep = ""),
           "\\delta"
           )
label <- paste("$", label, "$", sep = "")
# compute the graph
graph <- 
  foreach (
    i = 1:length(theta)
    ) %do% {
  theta_i <- theta[i]
  theta_i_list <- theta_i * seq(0.5, 1.5, by = 0.1)
  objective_i <- 
    foreach (
              j = 1:length(theta_i_list),
              .combine = "rbind"
             ) %do% {
               theta_ij <- theta_i_list[j]
               theta_j <- theta
               theta_j[i] <- theta_ij
               objective_ij <- 
                 compute_objective_simultaneous_entry(
                   Y, 
                   X, 
                   Z, 
                   EP_mc, 
                   NU_mc, 
                   theta_j
                   )
               return(objective_ij)
             }
  df_graph <- 
    data.frame(
      x = theta_i_list, 
      y = objective_i
      ) 
  g <- 
    ggplot(
    data = df_graph, 
    aes(
      x = x, 
      y = y
      )
    ) + 
    geom_point() +
    geom_vline(
      xintercept = theta_i, 
      linetype = "dotted"
      ) +
    ylab("objective function") + 
    xlab(TeX(label[i])) + 
    theme_classic()
  return(g)
}
saveRDS(
  graph, 
  file = "data/a6/A6_graph_simultaneous.rds"
  )
graph <- readRDS(file = "data/a6/A6_graph_simultaneous.rds")
graph
## [[1]]

## 
## [[2]]

## 
## [[3]]

## 
## [[4]]

## 
## [[5]]

  1. Estimate the parameters under the assumption of the sequential entry.
# sequential entry
theta <- 
  theta_sequential <-
  c(
    beta, 
    alpha, 
    delta, 
    rho
    )
Y <- Y_sequential
result_sequential <-
  optim(
        par = theta,
        fn = compute_objective_sequential_entry,
        method = "Nelder-Mead",
        Y = Y,
        X = X,
        Z = Z,
        EP_mc = EP_mc,
        NU_mc = NU_mc
        )
saveRDS(
  result_sequential, 
  file = "data/a6/A6_estimate_sequential.rds"
  )
result_sequential <- readRDS(file = "data/a6/A6_estimate_sequential.rds")
result_sequential
## $par
## [1] 0.7761887 0.2204343 1.0747480 2.0150864 0.9116741 0.2875538
## 
## $value
## [1] 0.2638
## 
## $counts
## function gradient 
##      233       NA 
## 
## $convergence
## [1] 0
## 
## $message
## NULL
comparison <-
  data.frame(
    actual = theta,
    estimate = result_sequential$par
  )
comparison
##      actual  estimate
## 1 0.6264538 0.7761887
## 2 0.1836433 0.2204343
## 3 0.8356286 1.0747480
## 4 1.5952808 2.0150864
## 5 1.0000000 0.9116741
## 6 0.3295078 0.2875538
  1. Estimate the parameters under the assumption of the simultaneous entry. Set the lower bound for \(\delta\) at 0.
# simultaneous entry
theta <- 
  theta_simultaneous <-
  c(
    beta, 
    alpha, 
    delta
    )
Y <- Y_simultaneous
result_simultaneous <-
  optim(
        par = theta,
        fn = compute_objective_simultaneous_entry,
        method = "Nelder-Mead",
        Y = Y,
        X = X,
        Z = Z,
        EP_mc = EP_mc,
        NU_mc = NU_mc)
saveRDS(
  result_simultaneous, 
  file = "data/a6/A6_estimate_simultaneous.rds"
  )
result_simultaneous <- readRDS(file = "data/a6/A6_estimate_simultaneous.rds")
result_simultaneous
## $par
## [1] 0.7347919 0.2151107 0.9427083 1.7495325 0.9448480
## 
## $value
## [1] 0.2158
## 
## $counts
## function gradient 
##      151       NA 
## 
## $convergence
## [1] 0
## 
## $message
## NULL
comparison <-
  data.frame(
    actual = theta,
    estimate = result_simultaneous$par
  )
comparison
##      actual  estimate
## 1 0.6264538 0.7347919
## 2 0.1836433 0.2151107
## 3 0.8356286 0.9427083
## 4 1.5952808 1.7495325
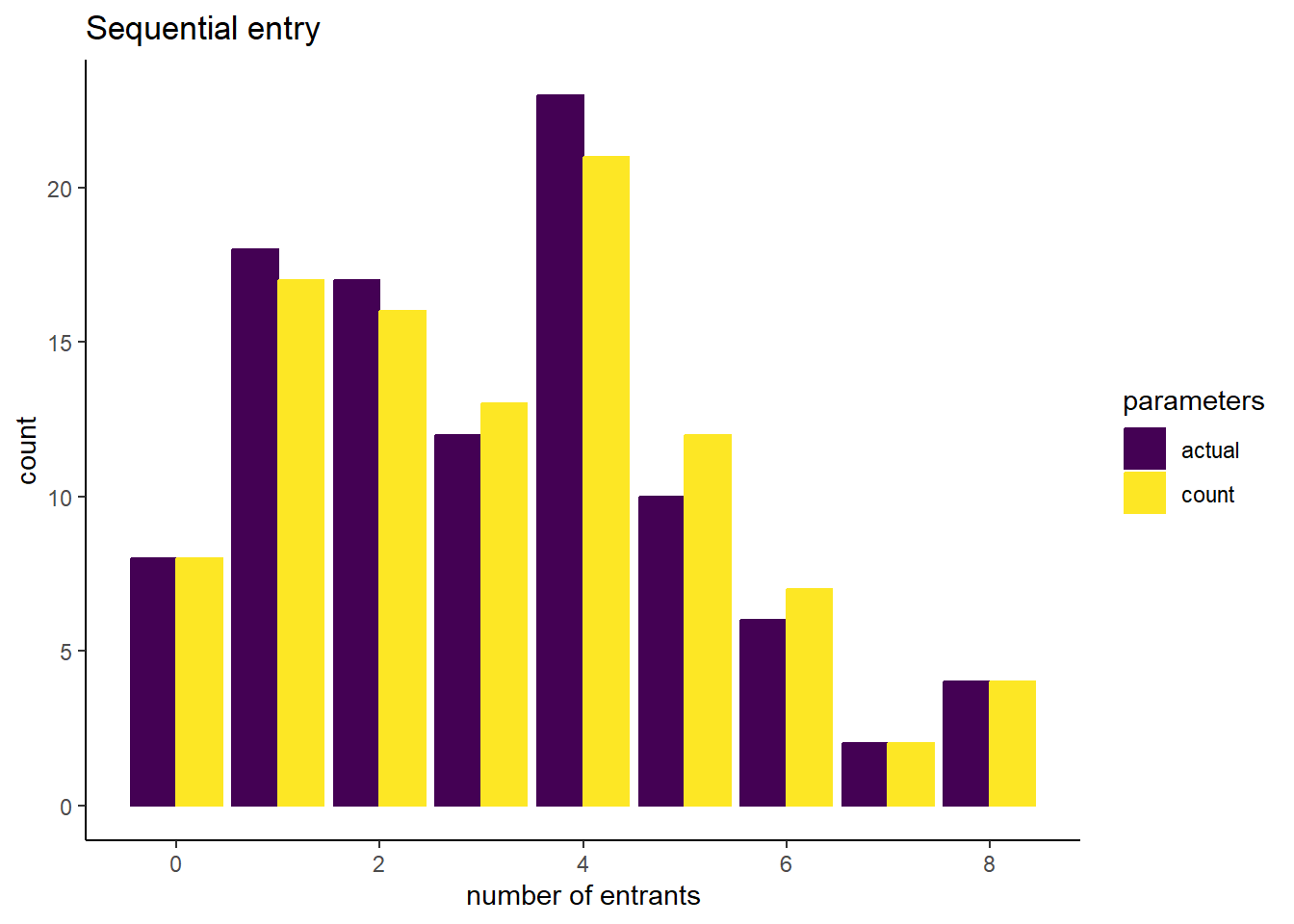
## 5 1.0000000 0.9448480

16.3 Conduct counterfactual simulations

  1. Fix the first draw of the Monte Carlo shocks. Suppose that the competitive effect becomes mild, i.e. \(\delta\) is changed to 0.5. Under these shocks, compute the equilibrium number of entrants across markets and plot the histogram with the estimated and counterfactual parameters. Conduct this analysis under the assumptions of sequential and simultaneous entry.